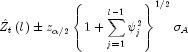Example 3: Forecasting

Consider the Wolfer Sunspot Data (Anderson 1971, p. 660) consisting of the number of sunspots observed each year from 1749 through 1924. The data set for this example consists of the number of sunspots observed from 1770 through 1869. Method forecast in class ARMA computes forecasts and 95-percent probability limits for the forecasts for an ARMA(2, 1) model fit using the method of moments option. With backward_origin = 3, forecast method provides forecasts given the data through 1866, 1867, 1868, and 1869, respectively. The deviations from the forecast for computing probability limits, and the psi weights can be used to update forecasts when more data is available. For example, the forecast for the 102-nd observation (year 1871) given the data through the 100-th observation (year 1869) is 77.21; and 95-percent probability limits are given by 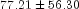$77.21 \pm 56.30$ . After observation 101 ( 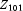$Z_{101}$ for year 1870) is available, the forecast can be updated by using

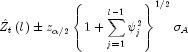
$\hat Z_t \left( l \right) \pm z_{\alpha /2} \left\{ {1 + \sum\limits_{j = 1}^{l - 1} {\psi _j^2 } } \right\}^{1/2} \sigma _A$

with the psi weight (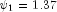 $\psi _1 = 1.37$ ) and the one-step-ahead forecast error for observation 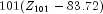$101 (Z_{101} - 83.72)$ to give the following:

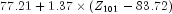
$77.21 + 1.37 \times (Z_{101} - 83.72)$

Since this updated forecast is one step ahead, the 95-percent probability limits are now given by the forecast 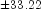$\pm 33.22$ .

import java.text.*;
import com.imsl.stat.*;
import com.imsl.math.PrintMatrix;
import com.imsl.math.PrintMatrixFormat;

public class ARMAEx3 {
    public static void main(String args[]) throws Exception {
        double[] z = {100.8, 81.6, 66.5, 34.8, 30.6, 7, 19.8, 92.5,
        154.4, 125.9, 84.8, 68.1, 38.5, 22.8, 10.2, 24.1, 82.9,
        132, 130.9, 118.1, 89.9, 66.6, 60, 46.9, 41, 21.3, 16,
        6.4, 4.1, 6.8, 14.5, 34, 45, 43.1, 47.5, 42.2, 28.1, 10.1,
        8.1, 2.5, 0, 1.4, 5, 12.2, 13.9, 35.4, 45.8, 41.1, 30.4,
        23.9, 15.7, 6.6, 4, 1.8, 8.5, 16.6, 36.3, 49.7, 62.5, 67,
        71, 47.8, 27.5, 8.5, 13.2, 56.9, 121.5, 138.3, 103.2,
        85.8, 63.2, 36.8, 24.2, 10.7, 15, 40.1, 61.5, 98.5, 124.3,
        95.9, 66.5, 64.5, 54.2, 39, 20.6, 6.7, 4.3, 22.8, 54.8,
        93.8, 95.7, 77.2, 59.1, 44, 47, 30.5, 16.3, 7.3, 37.3,
        73.9};
        PrintMatrixFormat pmf = new PrintMatrixFormat();
        
        ARMA arma = new ARMA(2, 1, z);
        arma.setRelativeError(0.0);
        arma.setMaxIterations(0);
        arma.compute();
        
        System.out.println("Method of Moments initial estimates:");
        new PrintMatrix("AR estimates are:  ").print(arma.getAR());
        System.out.println();
        new PrintMatrix("MA estimate is:  ").print(arma.getMA());
        arma.setBackwardOrigin(3);
        
        String[] labels = { "Forecast From 1866", "Forecast From 1867",
        "Forecast From 1868", "Forecast From 1869"};
        pmf.setColumnLabels(labels);
        new PrintMatrix("forecasts:  ").print(pmf, arma.forecast(12));
        
        String[] devlabel = {"Dev. for prob. limits"};
        pmf.setColumnLabels(devlabel);
        new PrintMatrix().print(pmf, arma.getDeviations());
        
        pmf = new PrintMatrixFormat();
        String[] psilabel = {"Psi"};
        pmf.setColumnLabels(psilabel);
        new PrintMatrix().print(pmf, arma.getPsiWeights());
    }
}

Output

Method of Moments initial estimates:
AR estimates are:  
     0     
0   1.244  
1  -0.575  


MA estimate is:  
     0     
0  -0.124  

                                    forecasts:  
    Forecast From 1866  Forecast From 1867  Forecast From 1868  Forecast From 1869  
 0        18.283              16.615              55.189              83.72         
 1        28.918              32.019              62.761              77.209        
 2        41.01               45.827              61.892              63.461        
 3        49.939              54.15               56.457              50.099        
 4        54.094              56.562              50.194              41.38         
 5        54.128              54.778              45.527              38.217        
 6        51.782              51.17               43.322              39.296        
 7        48.842              47.707              43.263              42.458        
 8        46.533              45.474              44.458              45.772        
 9        45.352              44.686              45.978              48.076        
10        45.21               44.991              47.183              49.037        
11        45.713              45.823              47.807              48.908        

    Dev. for prob. limits  
 0         33.218          
 1         56.298          
 2         67.617          
 3         70.643          
 4         70.751          
 5         71.087          
 6         71.907          
 7         72.534          
 8         72.75           
 9         72.765          
10         72.778          
11         72.823          

     Psi    
 0   1.368  
 1   1.127  
 2   0.616  
 3   0.118  
 4  -0.208  
 5  -0.326  
 6  -0.286  
 7  -0.169  
 8  -0.045  
 9   0.041  
10   0.077  
11   0.072

Link to Java source.