JMSL Chart Guide: Surface Plot

JMSL Chart Programmer's Guide

Surface Plot

The surface class is used to draw a surface. Surfaces can be specified either by an interface defining a function over a rectangle or by a set of points in three dimensions.

If a function defined over a rectangle is used, the function is evaluated on a rectangular grid of points. The resulting quadrilaterals are plotted.

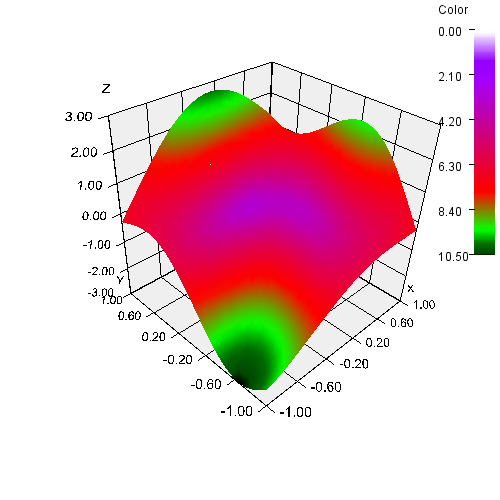
Shaded Surface

This example shades a surface with a user-specified function, instead of using shading. The same function is used as in the previous example:

z = 2sin (x + y) - cos (2x - 3y)

over the square [-1,1] by [-1,1].

The shade color function uses a Colormap object from the com.imsl.chart package. This maps a parameter to a color. In this example the surface is colored using the function

t = x2 + y2 + z2.

The function value is scaled to a colormap parameter using

s = t1/4 / 1.8.

The chart also includes a colormap legend, which is drawn on the background. It is positioned 5 pixels from the right edge and 5 pixels from the top edge of the canvas.

(Download Code)

import com.imsl.chart3d.*;
import com.imsl.chart.Colormap;

public class SampleShadedSurface extends JFrameChart3D
        implements Surface.ZFunction, ColorFunction {
    
    private Colormap colormap = Colormap.GREEN_RED_BLUE_WHITE;

    public SampleShadedSurface() { 
        Chart3D chart = getChart3D();
        AxisXYZ axis = new AxisXYZ(chart);
        Surface surface =
            new Surface(axis, this, -1.0, 1.0, -1.0, 1.0);
        surface.setColorFunction(this);
        surface.setSurfaceType(Surface.SURFACE_TYPE_NICEST);

        double maxColor = Math.pow(1.8,4);
        ColormapLegend colormapLegend =
                new ColormapLegend(chart, colormap, 0., maxColor);
        colormapLegend.setTitle("Color");
        colormapLegend.setPosition(-5, 5);
        render();
    }
    
    public double f(double x, double y) {
        return 2*Math.sin(x+y) - Math.cos(2*x-3*y);
    }
    
    public java.awt.Color color(double x, double y, double z) {
        double t = x*x + y*y + z*z ;
        double s = Math.pow(t, 0.25) / 1.8;
        return colormap.color(s);
    }

    public static void main(String args[]) {
        new SampleShadedSurface().setVisible(true);
    }
}