CrossCorrelation (JMSL Numerical Library)

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 4.0

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.stat
Class CrossCorrelation

java.lang.Object
  com.imsl.stat.CrossCorrelation

All Implemented Interfaces:: Cloneable, Serializable

public class CrossCorrelation
extends Object
implements Serializable, Cloneable

Computes the sample cross-correlation function of two stationary time series.

CrossCorrelation estimates the cross-correlation function of two jointly stationary time series given a sample of n = x.length observations ${X_t}$ and ${Y_t}$ for t = 1,2, ..., n.

Let

$hat mu _x = rm{xmean}$

be the estimate of the mean

of the time series ${X_t}$ where

$hat mu _X = left{ begin{array}{ll} mu _X & {rm for};mu _X; {rm known} \ frac{1}{n}sumlimits_{t=1}^n {X_t } & {rm for};mu _X; {rm unknown} end{array} right.$

The autocovariance function of ${X_t}$ , , is estimated by

$hat sigma _Xleft( k right) = frac{1}{n} sumlimits_{t = 1}^{n - k} {left( {X_t - hat mu _X} right)} left( {X_{t + k} - hat mu _X} right), mbox{hspace{20pt}k=0,1,dots,K}$

where K = maximum_lag. Note that

is equivalent to the sample variance of x returned by method getVarianceX. The autocorrelation function

is estimated by

$hatrho _X(k) = frac{hat sigma _X(k)}{hat sigma _X(0)},mbox{hspace{20pt}} k=0,1,dots,K$

Note that by definition. Let

$hat mu _Y = {rm ymean}, hat sigma _Y(k), {rm and} hat rho _Y(k)$

be similarly defined.

The cross-covariance function $sigma _{XY}(k)$ is estimated by

$hat sigma _{XY}(k) = left{ begin{array}{ll} frac{1}{n}sumlimits_{t=1}^{n-k}(X_t - {hat mu _X})(Y_{t+k} - {hatmu _Y}) &{k = 0,1, dots,K} \ frac{1}{n}sumlimits_{t=1-k}^{n}(X_t - {hat mu _X})(Y_{t+k} - {hatmu _Y}) &{k = -1,-2, dots,-K} end {array} right.$

The cross-correlation function $rho _{XY}(k)$ is estimated by

$hat rho _{XY}(k) = frac{hat sigma _{XY}(k)} {[hatsigma _X(0) hatsigma _Y(0) ]^{frac{1}{2}}} ;;; {k = 0,pm1, dots,pm K}$

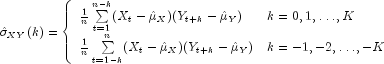
The standard errors of the sample cross-correlations may be optionally computed according to the getStandardErrors method argument stderrMethod. One method is based on a general asymptotic expression for the variance of the sample cross-correlation coefficient of two jointly stationary time series with independent, identically distributed normal errors given by Bartlet (1978, page 352). The theoretical formula is

$begin{array}{c} {rm var} left { hat rho _{XY}(k) right } = frac{1}{n-k}sumlimits_{i=-infty}^{infty} left [right. {rho _X(i)}+rho _{XY}(i-k)rho _{XY}(i+k) \ -2rho _{XY}(k){rho _X(i)rho _{XY}(i+k)+rho _{XY}(-i)rho _Y(i+k)} \ +rho^2_{XY}(k){rho_X(i) + frac{1}{2}rho^2_X(i) + frac{1}{2}rho^2_Y(i)} left. right ] end{array}$

For computational purposes, the autocorrelations

and

and the cross-correlations $rho _{XY}(k)$ are replaced by their corresponding estimates for

, and the limits of summation are equal to zero for all k such that

A second method evaluates Bartlett's formula under the additional assumption that the two series have no cross-correlation. The theoretical formula is

${rm var}{hat rho_{XY}(k)} = frac{1}{n-k}sumlimits_{i=-infty}^{infty}{rho_X(i)rho_Y(i)} ;;;;; {k ge 0}$

For additional special cases of Bartlett's formula, see Box and Jenkins (1976, page 377).

An important property of the cross-covariance coefficient is $sigma _{XY}(k) = sigma _{YX}(-k)$ for . This result is used in the computation of the standard error of the sample cross-correlation for lag . In general, the cross-covariance function is not symmetric about zero so both positive and negative lags are of interest.

See Also:: Example, Serialized Form

Nested Class Summary
`static class`	`CrossCorrelation.NonPosVariancesException` The problem is ill-conditioned.

Field Summary
`static int`	`BARTLETTS_FORMULA` Indicates standard error computation using Bartlett's formula.
`static int`	`BARTLETTS_FORMULA_NOCC` Indicates standard error computation using Bartlett's formula with the assumption of no cross-correlation.

Constructor Summary
`CrossCorrelation(double[] x, double[] y, int maximum_lag)` Constructor to compute the sample cross-correlation function of two stationary time series.

Method Summary
`double[]`	`getAutoCorrelationX()` Returns the autocorrelations of the time series `x`.
`double[]`	`getAutoCorrelationY()` Returns the autocorrelations of the time series `y`.
`double[]`	`getAutoCovarianceX()` Returns the autocovariances of the time series `x`.
`double[]`	`getAutoCovarianceY()` Returns the autocovariances of the time series `y`.
`double[]`	`getCrossCorrelation()` Returns the cross-correlations between the time series `x` and `y`.
`double[]`	`getCrossCovariance()` Returns the cross-covariances between the time series `x` and `y`.
`double`	`getMeanX()` Returns the mean of the time series `x`.
`double`	`getMeanY()` Returns the mean of the time series `y`.
`double[]`	`getStandardErrors(int stderrMethod)` Returns the standard errors of the cross-correlations between the time series `x` and `y`.
`double`	`getVarianceX()` Returns the variance of time series `x`.
`double`	`getVarianceY()` Returns the variance of time series `y`.
`void`	`setMeanX(double mean)` Estimate of the mean of time series `x`.
`void`	`setMeanY(double mean)` Estimate of the mean of time series `y`.

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Field Detail

BARTLETTS_FORMULA

public static final int BARTLETTS_FORMULA

Indicates standard error computation using Bartlett's formula.

See Also:: Constant Field Values

BARTLETTS_FORMULA_NOCC

public static final int BARTLETTS_FORMULA_NOCC

Indicates standard error computation using Bartlett's formula with the assumption of no cross-correlation.

See Also:: Constant Field Values

Constructor Detail

CrossCorrelation

public CrossCorrelation(double[] x,
                        double[] y,
                        int maximum_lag)

Constructor to compute the sample cross-correlation function of two stationary time series.
Parameters:: x - A one-dimensional double array containing the first stationary time series.; y - A one-dimensional double array containing the second stationary time series.; maximum_lag - An int containing the maximum lag of the cross-covariance and cross-correlations to be computed. maximum_lag must be greater than or equal to 1 and less than the minimum of the number of observations of x and y.

Method Detail

getAutoCorrelationX

public double[] getAutoCorrelationX()
                             throws CrossCorrelation.NonPosVariancesException

Returns the autocorrelations of the time series x.

Returns:: A double array of length maximum_lag +1 containing the autocorrelations of the time series x. The 0-th element of this array is 1. The k-th element of this array contains the autocorrelation of lag k where k = 1, ..., maximum_lag.
Throws:: CrossCorrelation.NonPosVariancesException

getAutoCorrelationY

public double[] getAutoCorrelationY()
                             throws CrossCorrelation.NonPosVariancesException

Returns the autocorrelations of the time series y.

Returns:: A double array of length maximum_lag +1 containing the autocorrelations of the time series y. The 0-th element of this array is 1. The k-th element of this array contains the autocorrelation of lag k where k = 1, ..., maximum_lag.
Throws:: CrossCorrelation.NonPosVariancesException

getAutoCovarianceX

public double[] getAutoCovarianceX()
                            throws CrossCorrelation.NonPosVariancesException

Returns the autocovariances of the time series x.

Returns:: A double array of length maximum_lag +1 containing the variances and autocovariances of the time series x. The 0-th element of the array contains the variance of the time series x. The k-th element contains the autocovariance of lag k where k = 1, ..., maximum_lag.
Throws:: CrossCorrelation.NonPosVariancesException

getAutoCovarianceY

public double[] getAutoCovarianceY()
                            throws CrossCorrelation.NonPosVariancesException

Returns the autocovariances of the time series y.

Returns:: A double array of length maximum_lag +1 containing the variances and autocovariances of the time series y. The 0-th element of the array contains the variance of the time series x. The k-th element contains the autocovariance of lag k where k = 1, ..., maximum_lag.
Throws:: CrossCorrelation.NonPosVariancesException

getCrossCorrelation

public double[] getCrossCorrelation()
                             throws CrossCorrelation.NonPosVariancesException

Returns the cross-correlations between the time series x and y.

Returns:: A double array of length 2 * maximum_lag +1 containing the cross-correlations between the time series x and y. The cross-correlation between x and y at lag k, where k = -maximum_lag ,..., 0, 1,...,maximum_lag, corresponds to output array indices 0, 1,..., (2*maximum_lag).
Throws:: CrossCorrelation.NonPosVariancesException

getCrossCovariance

public double[] getCrossCovariance()

Returns the cross-covariances between the time series x and y.

Returns:: A double array of length 2 * maximum_lag +1 containing the cross-covariances between the time series x and y. The cross-covariance between x and y at lag k, where k = -maximum_lag ,..., 0, 1,...,maximum_lag, corresponds to output array indices 0, 1,..., (2*maximum_lag).

getMeanX

public double getMeanX()

Returns the mean of the time series x.

Returns:: A double containing the mean of the time series x.

getMeanY

public double getMeanY()

Returns the mean of the time series y.

Returns:: A double containing the mean of the time series y.

getStandardErrors

public double[] getStandardErrors(int stderrMethod)
                           throws CrossCorrelation.NonPosVariancesException

Returns the standard errors of the cross-correlations between the time series x and y. Method of computation for standard errors of the cross-correlation is determined by the stderrMethod parameter. If stderrMethod is set to BARTLETTS_FORMULA, Bartlett's formula is used to compute the standard errors of cross-correlations. If stderrMethod is set to BARTLETTS_FORMULA_NOCC, Bartlett's formula is used to compute the standard errors of cross-correlations, with the assumption of no cross-correlation.

Parameters:: stderrMethod - An int specifying the method to compute the standard errors of cross-correlations between the time series x and y.
Returns:: A double array of length 2 * maximum_lag + 1 containing the standard errors of the cross-correlations between the time series x and y. The standard error of cross-correlations between x and y at lag k, where k = -maximum_lag,..., 0, 1,..., maximum_lag, corresponds to output array indices 0, 1,..., (2*maximum_lag).
Throws:: CrossCorrelation.NonPosVariancesException

getVarianceX

public double getVarianceX()
                    throws CrossCorrelation.NonPosVariancesException

Returns the variance of time series x.

Returns:: A double containing the variance of the time series x.
Throws:: CrossCorrelation.NonPosVariancesException

getVarianceY

public double getVarianceY()
                    throws CrossCorrelation.NonPosVariancesException

Returns the variance of time series y.

Returns:: A double containing the variance of the time series y.
Throws:: CrossCorrelation.NonPosVariancesException

setMeanX

public void setMeanX(double mean)

Estimate of the mean of time series x.

Parameters:: mean - A double containing the estimate mean of the time series x.

setMeanY

public void setMeanY(double mean)

Estimate of the mean of time series y.

Parameters:: mean - A double containing the estimate mean of the time series y.