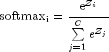Activation (JMSL Numerical Library)

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 4.0

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.datamining.neural
Interface Activation

All Superinterfaces:: Serializable

public interface Activation
extends Serializable

Interface implemented by perceptron activation functions.

Standard activation functions are defined as static members of this interface. New activation functions can be defined by implementing a method, g(double x), returning the value and a method, derivative(double x, double y), returning the derivative of g evaluated at x where y = g(x).

See Also:: Feed Forward Class Example 1, Perceptron

Field Summary
`static Activation`	`LINEAR` The identity activation function, g(x) = x.
`static Activation`	`LOGISTIC` The logistic activation function, $g(x)=frac{1}{1+e^{-x}}$ .
`static Activation`	`LOGISTIC_TABLE` The logistic activation function computed using a table.
`static long`	`serialVersionUID`
`static Activation`	`SOFTMAX` The softmax activation function.
`static Activation`	`SQUASH` The squash activation function, $g(x) = frac{x}{1+\|x\|}$
`static Activation`	`TANH` The hyperbolic tangent activation function, $g(x)=tanh{x}= frac{e^x-e^{-x}}{e^x+e^{-x}}$ .

Method Summary
`double`	`derivative(double x, double y)` Returns the value of the derivative of the activation function.
`double`	`g(double x)` Returns the value of the activation function.

Field Detail

LINEAR

public static final Activation LINEAR

The identity activation function, g(x) = x.

LOGISTIC

public static final Activation LOGISTIC

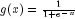The logistic activation function, $g(x)=frac{1}{1+e^{-x}}$ .

LOGISTIC_TABLE

public static final Activation LOGISTIC_TABLE

The logistic activation function computed using a table. This is an approximation to the logistic function that is faster to compute.

This version of the logistic function differs from the exact version by at most 4.0e-9.

Networks trained using this activation should not use Activation.LOGISTIC for forecasting. Forecasting should be done using the specific function supplied during training.

serialVersionUID

public static final long serialVersionUID

See Also:: Constant Field Values

SOFTMAX

public static final Activation SOFTMAX

The softmax activation function.

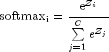
${rm{softmax}}_{rm{i}}=frac{{{mathop{rm e}nolimits} ^{Z_i } }} {{sumlimits_{j = 1}^C {e^{Z_j } } }}$

SQUASH

public static final Activation SQUASH

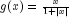
The squash activation function, $g(x) = frac{x}{1+|x|}$

TANH

public static final Activation TANH

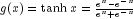The hyperbolic tangent activation function, $g(x)=tanh{x}= frac{e^x-e^{-x}}{e^x+e^{-x}}$ .

Method Detail

derivative

public double derivative(double x,
                         double y)

Returns the value of the derivative of the activation function.

Parameters:: x - A double which specifies the point at which the activation function is to be evaluated.; y - A double which specifies y = g(x), the value of the activation function at x. This parameter is not mathematically required, but can sometimes be used to more quickly compute the derivative.
Returns:: A double containing the value of the derivative of the activation function at x.

g

public double g(double x)

Returns the value of the activation function.

Parameters:: x - A double is the point at which the activation function is to be evaluated.
Returns:: A double containing the value of the activation function at x.