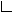Cdf (JMSL Numerical Library)

Overview

Package

Class

Tree

Index

Help

JMSL^TM Numerical Library 4.0

PREV CLASS NEXT CLASS

FRAMES NO FRAMES

SUMMARY: NESTED | FIELD | CONSTR | METHOD

DETAIL: FIELD | CONSTR | METHOD

com.imsl.stat
Class Cdf

java.lang.Object
  com.imsl.stat.Cdf

public final class Cdf
extends Object

Cumulative probability distribution functions, probability density functions, and their inverses.

See Also:: Example

Method Summary
`static double`	`beta(double x, double pin, double qin)` Evaluates the beta cumulative probability distribution function.
`static double`	`betaMean(double pin, double qin)` Evaluates the mean of the beta cumulative probability distribution function
`static double`	`betaProb(double x, double pin, double qin)` Evaluates the beta probability density function.
`static double`	`betaVariance(double pin, double qin)` Evaluates the variance of the beta cumulative probability distribution function
`static double`	`binomial(int k, int n, double p)` Evaluates the binomial cumulative probability distribution function.
`static double`	`binomialProb(int k, int n, double p)` Evaluates the binomial probability density function.
`static double`	`bivariateNormal(double x, double y, double rho)` Evaluates the bivariate normal cumulative probability distribution function.
`static double`	`chi(double chsq, double df)` Evaluates the chi-squared cumulative probability distribution function.
`static double`	`chiMean(double df)` Evaluates the mean of the chi-squared cumulative probability distribution function
`static double`	`chiProb(double chsq, double df)` Evaluates the chi-squared probability density function
`static double`	`chiVariance(double df)` Evaluates the variance of the chi-squared cumulative probability distribution function
`static double`	`discreteUniform(int x, int n)` Evaluates the discrete uniform cumulative probability distribution function.
`static double`	`discreteUniformProb(int x, int n)` Evaluates the discrete uniform probability density function.
`static double`	`exponential(double x, double scale)` Evaluates the exponential cumulative probability distribution function.
`static double`	`exponentialProb(double x, double scale)` Evaluates the exponential probability density function
`static double`	`extremeValue(double x, double mu, double beta)` Evaluates the extreme value cumulative probability distribution function.
`static double`	`extremeValueProb(double x, double mu, double beta)` Evaluates the extreme value probability density function.
`static double`	`F(double x, double dfn, double dfd)` Evaluates the F cumulative probability distribution function.
`static double`	`FProb(double x, double dfn, double dfd)` Evaluates the F probability density function.
`static double`	`gamma(double x, double a)` Evaluates the gamma cumulative probability distribution function.
`static double`	`gammaProb(double x, double a, double b)` Evaluates the gamma probability density function.
`static double`	`geometric(int x, double p)` Evaluates the discrete geometric cumulative probability distribution function.
`static double`	`geometricProb(int x, double p)` Evaluates the discrete geometric probability density function.
`static double`	`hypergeometric(int k, int sampleSize, int defectivesInLot, int lotSize)` Evaluates the hypergeometric cumulative probability distribution function.
`static double`	`hypergeometricProb(int k, int sampleSize, int defectivesInLot, int lotSize)` Evaluates the hypergeometric probability density function.
`static double`	`inverseBeta(double p, double pin, double qin)` Evaluates the inverse of the beta cumulative probability distribution function.
`static double`	`inverseChi(double p, double df)` Evaluates the inverse of the chi-squared cumulative probability distribution function.
`static int`	`inverseDiscreteUniform(double p, int n)` Returns the inverse of the discrete uniform cumulative probability distribution function.
`static double`	`inverseExponential(double p, double scale)` Evaluates the inverse of the exponential cumulative probability distribution function.
`static double`	`inverseExtremeValue(double p, double mu, double beta)` Returns the inverse of the extreme value cumulative probability distribution function.
`static double`	`inverseF(double p, double dfn, double dfd)` Returns the inverse of the F cumulative probability distribution function.
`static double`	`inverseGamma(double p, double a)` Evaluates the inverse of the gamma cumulative probability distribution function.
`static double`	`inverseGeometric(double r, double p)` Returns the inverse of the discrete geometric cumulative probability distribution function.
`static double`	`inverseLogNormal(double p, double mu, double sigma)` Returns the inverse of the standard lognormal cumulative probability distribution function.
`static double`	`inverseNoncentralchi(double p, double df, double alam)` Evaluates the inverse of the noncentral chi-squared cumulative probability distribution function.
`static double`	`inverseNoncentralstudentsT(double p, int idf, double delta)` Evaluates the inverse of the noncentral Student's t cumulative probability distribution function.
`static double`	`inverseNormal(double p)` Evaluates the inverse of the normal (Gaussian) cumulative probability distribution function.
`static double`	`inverseRayleigh(double p, double alpha)` Returns the inverse of the Rayleigh cumulative probability distribution function.
`static double`	`inverseStudentsT(double p, double df)` Returns the inverse of the Student's t cumulative probability distribution function.
`static double`	`inverseUniform(double p, double aa, double bb)` Returns the inverse of the uniform cumulative probability distribution function.
`static double`	`inverseWeibull(double p, double gamma, double alpha)` Returns the inverse of the Weibull cumulative probability distribution function.
`static double`	`logNormal(double x, double mu, double sigma)` Evaluates the standard lognormal cumulative probability distribution function.
`static double`	`logNormalProb(double x, double mu, double sigma)` Evaluates the standard lognormal probability density function.
`static double`	`noncentralchi(double chsq, double df, double alam)` Evaluates the noncentral chi-squared cumulative probability distribution function.
`static double`	`noncentralstudentsT(double t, int idf, double delta)` Evaluates the noncentral Student's t cumulative probability distribution function.
`static double`	`normal(double x)` Evaluates the normal (Gaussian) cumulative probability distribution function.
`static double`	`poisson(int k, double theta)` Evaluates the Poisson cumulative probability distribution function.
`static double`	`poissonProb(int k, double theta)` Evaluates the Poisson probability density function.
`static double`	`Rayleigh(double x, double alpha)` Evaluates the Rayleigh cumulative probability distribution function.
`static double`	`RayleighProb(double x, double alpha)` Evaluates the Rayleigh probability density function.
`static double`	`studentsT(double t, double df)` Evaluates the Student's t cumulative probability distribution function.
`static double`	`uniform(double x, double aa, double bb)` Evaluates the uniform cumulative probability distribution function.
`static double`	`Weibull(double x, double gamma, double alpha)` Evaluates the Weibull cumulative probability distribution function.
`static double`	`WeibullProb(double x, double gamma, double alpha)` Evaluates the Weibull probability density function.

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Method Detail

beta

public static double beta(double x,
                          double pin,
                          double qin)

Evaluates the beta cumulative probability distribution function.

Method beta evaluates the distribution function of a beta random variable with parameters pin and qin. This function is sometimes called the incomplete beta ratio and, with p = pin and q = qin, is denoted by . It is given by

$I_x left( {p,,q} right) = frac{{Gamma left( p right)Gamma left( q right)}}{{Gamma left( {p + q} right)}}int_0^x {,t^{p - 1} left( {1 - t} right)^{q - 1} dt}$

where is the gamma function. The value of the distribution function is the probability that the random variable takes a value less than or equal to x.

The integral in the expression above is called the incomplete beta function and is denoted by . The constant in the expression is the reciprocal of the beta function (the incomplete function evaluated at one) and is denoted by .

beta uses the method of Bosten and Battiste (1974).

Plot of Beta Distribution Function

Parameters:: x - a double, the argument at which the function is to be evaluated.; pin - a double, the first beta distribution parameter.; qin - a double, the second beta distribution parameter.
Returns:: a double, the probability that a beta random variable takes on a value less than or equal to x.
See Also:: Example

betaMean

public static double betaMean(double pin,
                              double qin)

Evaluates the mean of the beta cumulative probability distribution function

Parameters:: pin - a double, the first beta distribution parameter.; qin - a double, the second beta distribution parameter.
Returns:: a double, the mean of the beta distribution function.

betaProb

public static double betaProb(double x,
                              double pin,
                              double qin)

Evaluates the beta probability density function.

Parameters:: x - a double, the argument at which the function is to be evaluated.; pin - a double, the first beta distribution parameter.; qin - a double, the second beta distribution parameter.
Returns:: a double, the value of the probability density function at x.

betaVariance

public static double betaVariance(double pin,
                                  double qin)

Evaluates the variance of the beta cumulative probability distribution function

Parameters:: pin - a double, the first beta distribution parameter.; qin - a double, the second beta distribution parameter.
Returns:: a double, the variance of the beta distribution function.

binomial

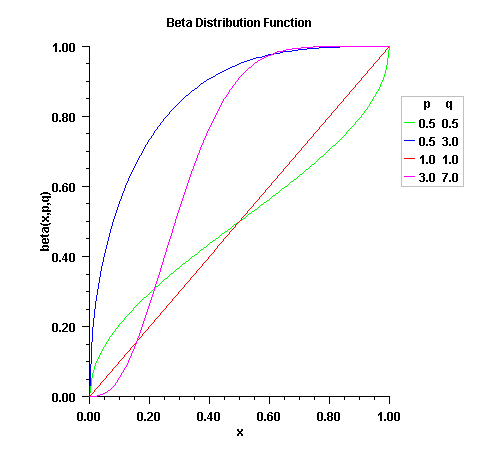
public static double binomial(int k,
                              int n,
                              double p)

Evaluates the binomial cumulative probability distribution function.

Method binomial evaluates the distribution function of a binomial random variable with parameters n and p. It does this by summing probabilities of the random variable taking on the specific values in its range. These probabilities are computed by the recursive relationship

$Pr left( {X = j} right) = frac{{left( {n + 1 - j} right)p}}{{jleft( {1 - p} right)}}Pr left( {X = j - 1} right)$

To avoid the possibility of underflow, the probabilities are computed forward from 0, if k is not greater than n times p, and are computed backward from n, otherwise. The smallest positive machine number, , is used as the starting value for summing the probabilities, which are rescaled by if forward computation is performed and by if backward computation is done. For the special case of p = 0, binomial is set to 1; and for the case p = 1, binomial is set to 1 if k = n and to 0 otherwise.

Parameters:: k - the int argument for which the binomial distribution function is to be evaluated.; n - the int number of Bernoulli trials.; p - a double scalar value representing the probability of success on each trial.
Returns:: a double scalar value representing the probability that a binomial random variable takes a value less than or equal to k. This value is the probability that k or fewer successes occur in n independent Bernoulli trials, each of which has a p probability of success.
See Also:: Example

binomialProb

public static double binomialProb(int k,
                                  int n,
                                  double p)

Evaluates the binomial probability density function.

Method binomialProb evaluates the probability that a binomial random variable with parameters n and p takes on the value k. It does this by computing probabilities of the random variable taking on the values in its range less than (or the values greater than) k. These probabilities are computed by the recursive relationship

$Pr left( {X = j} right) = frac{{left( {n + 1 - j} right)p}}{{jleft( {1 - p} right)}}Pr left( {X = j - 1} right)$

To avoid the possibility of underflow, the probabilities are computed forward from 0, if k is not greater than , and are computed backward from n, otherwise. The smallest positive machine number, , is used as the starting value for computing the probabilities, which are rescaled by if forward computation is performed and by if backward computation is done.

For the special case of p = 0, binomialProb is set to 0 if k is greater than 0 and to 1 otherwise; and for the case p = 1, binomialProb is set to 0 if k is less than n and to 1 otherwise.

Plot of Binomial Probability Function

Parameters:: k - the int argument for which the binomial distribution function is to be evaluated.; n - the int number of Bernoulli trials.; p - a double scalar value representing the probability of success on each trial.
Returns:: a double scalar value representing the probability that a binomial random variable takes a value equal to k.
See Also:: Example

bivariateNormal

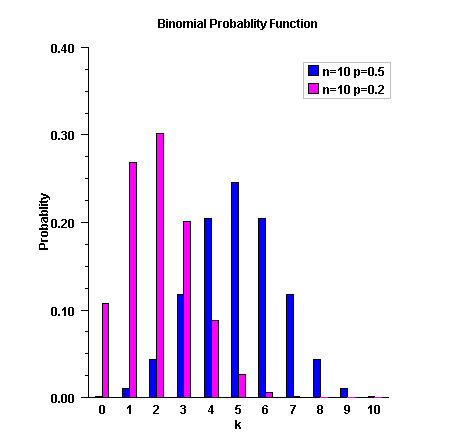
public static double bivariateNormal(double x,
                                     double y,
                                     double rho)

Evaluates the bivariate normal cumulative probability distribution function. Let

be a bivariate normal variable with mean

and variance-covariance matrix

$left[ begin{array}{cc} 1 & rho \ rho & 1end{array}right]$

This method computes the probability that

and

Plot of Bivariate Normal Distribution Function

Parameters:: x - is the x-coordinate of the point for which the bivariate normal distribution function is to be evaluated.; y - is the y-coordinate of the point for which the bivariate normal distribution function is to be evaluated.; rho - is the correlation coefficient.
Returns:: the probability that a bivariate normal random variable with correlation rho satisfies and .

chi

public static double chi(double chsq,
                         double df)

Evaluates the chi-squared cumulative probability distribution function.

Method chi evaluates the distribution function, F, of a chi-squared random variable with df degrees of freedom, that is, with , and ,

$Fleft( x right) = frac{1}{{2^{nu /2} Gamma left( {nu /2} right)}} int_0^x {e^{ - t/2} t^{nu /2 - 1} } dt$

where is the gamma function. The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.

For , chi uses the Wilson-Hilferty approximation (Abramowitz and Stegun 1964, equation 26.4.17) to the normal distribution, and method normal is used to evaluate the normal distribution function.

For , chi uses series expansions to evaluate the distribution function. If , chi uses the series 6.5.29 in Abramowitz and Stegun (1964), otherwise, it uses the asymptotic expansion 6.5.32 in Abramowitz and Stegun.

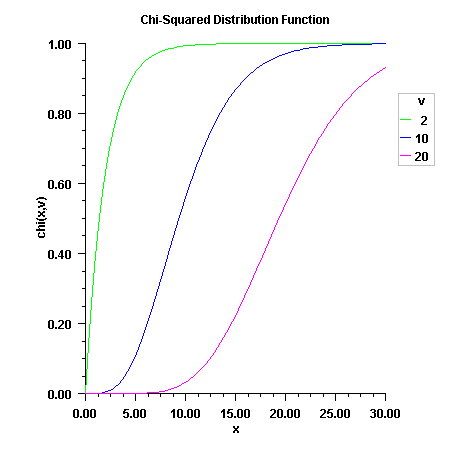
Plot of Chi-Squared Distribution Function

Parameters:: chsq - a double scalar value representing the argument at which the function is to be evaluated.; df - a double scalar value representing the number of degrees of freedom. This must be at least 0.5.
Returns:: a double scalar value representing the probability that a chi-squared random variable takes a value less than or equal to chsq.
See Also:: Example

chiMean

public static double chiMean(double df)

Evaluates the mean of the chi-squared cumulative probability distribution function

Parameters:: df - a double scalar value representing the number of degrees of freedom. This must be at least 0.5.
Returns:: a double, the mean of the chi-squared distribution function.

chiProb

public static double chiProb(double chsq,
                             double df)

Evaluates the chi-squared probability density function

Parameters:: chsq - a double scalar value representing the argument at which the function is to be evaluated.; df - a double scalar value representing the number of degrees of freedom. This must be at least 0.5.
Returns:: a double scalar value, the value of the probability density function at chsq.

chiVariance

public static double chiVariance(double df)

Evaluates the variance of the chi-squared cumulative probability distribution function

Parameters:: df - a double scalar value representing the number of degrees of freedom. This must be at least 0.5.
Returns:: a double, the variance of the chi-squared distribution function.

discreteUniform

public static double discreteUniform(int x,
                                     int n)

Evaluates the discrete uniform cumulative probability distribution function.

Parameters:: x - an int scalar value representing the argument at which the function is to be evaluated. x should be a value between the lower limit 0 and upper limit n; n - an int scalar value representing the upper limit of the discrete uniform distribution.
Returns:: a double scalar value representing the probability that a discrete uniform random variable takes a value less than or equal to x.

discreteUniformProb

public static double discreteUniformProb(int x,
                                         int n)

Evaluates the discrete uniform probability density function.

Parameters:: x - an int argument for which the discrete uniform probability density function is to be evaluated. x should be a value between the lower limit 0 and upper limit n; n - an int scalar value representing the upper limit of the discrete uniform distribution.
Returns:: a double scalar value representing the probability that a discrete uniform random variable takes a value equal to x.
See Also:: Example

exponential

public static double exponential(double x,
                                 double scale)

Evaluates the exponential cumulative probability distribution function.

Method exponential is a special case of the gamma distribution function, which evaluates the distribution function, F, with scale parameter b and shape parameter a, used in the gamma distribution function equal to 1.0. That is,

$Fleft( x right) = frac{1}{{Gamma left( a right)}}int_0^x {e^{ - t/b}} dt$

where is the gamma function. (The gamma function is the integral from 0 to of the same integrand as above). The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.

If x is less than or equal to 1.0, gamma uses a series expansion. Otherwise, a continued fraction expansion is used. (See Abramowitz and Stegun, 1964.)

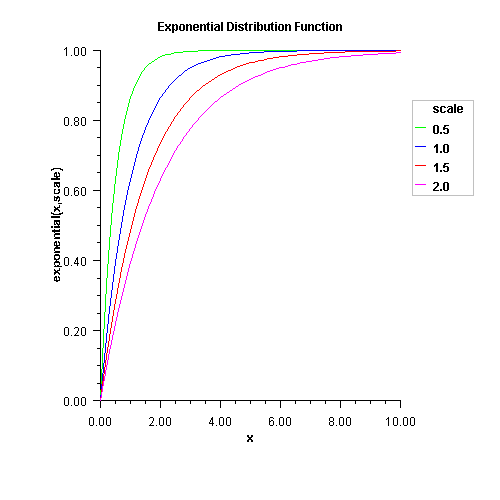
Plot of Exponential Distribution Function

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated.; scale - a double scalar value representing the scale parameter, .
Returns:: a double scalar value representing the probability that an exponential random variable takes on a value less than or equal to x.
See Also:: Example

exponentialProb

public static double exponentialProb(double x,
                                     double scale)

Evaluates the exponential probability density function

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated.; scale - a double scalar value representing the scale parameter.
Returns:: a double scalar value, the value of the probability density function at x.

extremeValue

public static double extremeValue(double x,
                                  double mu,
                                  double beta)

Evaluates the extreme value cumulative probability distribution function.

Method extremeValue, also known as the Gumbel minimum distribution, evaluates the extreme value distribution function, F, of a uniform random variable with location parameter and shape parameter ; that is,

$Fleft( x right) = int_0^x {1 - e^{ - e^{frac{x-mu}{beta}}}} dt$

The case where and is called the standard Gumbel distribution.

Random numbers are generated by evaluating uniform variates , equating the continuous distribution function, and then solving for by first computing $frac{x_i - mu}{beta}=log(-log(1-u_i))$ .

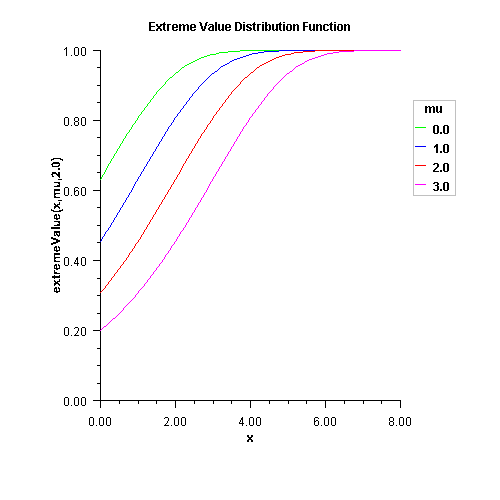
Plot of Extreme Value Distribution Function

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated.; mu - a double scalar value representing the location parameter, .; beta - a double scalar value representing the scale parameter,
Returns:: a double scalar value representing the probability that an extreme value random variable takes on a value less than or equal to x.
See Also:: Example

extremeValueProb

public static double extremeValueProb(double x,
                                      double mu,
                                      double beta)

Evaluates the extreme value probability density function.

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated.; mu - a double scalar value representing the location parameter.; beta - a double scalar value representing the scale parameter.
Returns:: a double scalar value representing the probability density function at x.
See Also:: Example

F

public static double F(double x,
                       double dfn,
                       double dfd)

Evaluates the F cumulative probability distribution function.

F evaluates the distribution function of a Snedecor's F random variable with dfn numerator degrees of freedom and dfd denominator degrees of freedom. The function is evaluated by making a transformation to a beta random variable and then using the function beta. If X is an F variate with and degrees of freedom and , then Y is a beta variate with parameters and . F also uses a relationship between F random variables that can be expressed as follows:

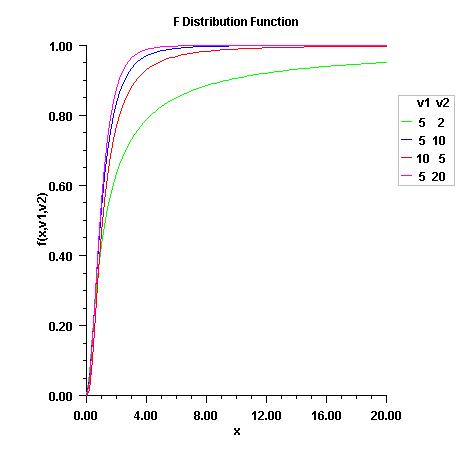
Plot of F Distribution Function

Parameters:: x - a double, the argument at which the function is to be evaluated.; dfn - a double, the numerator degrees of freedom. It must be positive.; dfd - a double, the denominator degrees of freedom. It must be positive.
Returns:: a double, the probability that an F random variable takes on a value less than or equal to x.
See Also:: Example

FProb

public static double FProb(double x,
                           double dfn,
                           double dfd)

Evaluates the F probability density function.

The probability density function of the F distribution is

${it f}(x, {it dfn}, {it dfd})= {frac { {Gamma}(frac {v_1 + v_2}{2})({frac {v_1}{v_2})}^{frac{v_1}{2}} x^{frac {v_1}{2}} } {{{Gamma}(frac {v_1}{2}) }{{Gamma}(frac {v_2}{2}) } {(1+frac{v_1x}{v_2})}^{frac{v_1+v_2}{2} } }}$

where

and

are the shape parameters dfn and dfd and

is the gamma function,

${Gamma (a)} = {int}_{0}^{infty}{t^{a-1} e^{-t } it dt}$

Parameters:: x - a double, the argument at which the function is to be evaluated.; dfn - a double, the numerator degrees of freedom. It must be positive.; dfd - a double, the denominator degrees of freedom. It must be positive.
Returns:: a double, the value of the probability density function at x.

gamma

public static double gamma(double x,
                           double a)

Evaluates the gamma cumulative probability distribution function.

Method gamma evaluates the distribution function, F, of a gamma random variable with shape parameter a; that is,

$Fleft( x right) = frac{1}{{Gamma left( a right)}}int_0^x {e^{ - t} t^{a - 1} } dt$

The gamma distribution is often defined as a two-parameter distribution with a scale parameter b (which must be positive), or even as a three-parameter distribution in which the third parameter c is a location parameter. In the most general case, the probability density function over is

$fleft( t right) = frac{1}{{b^a Gamma left( a right)}}e^{ - left( {t - c} right)/b} left( {x - c} right)^{a - 1}$

If T is such a random variable with parameters a, b, and c, the probability that can be obtained from gamma by setting .

If X is less than a or if X is less than or equal to 1.0, gamma uses a series expansion. Otherwise, a continued fraction expansion is used. (See Abramowitz and Stegun, 1964.)

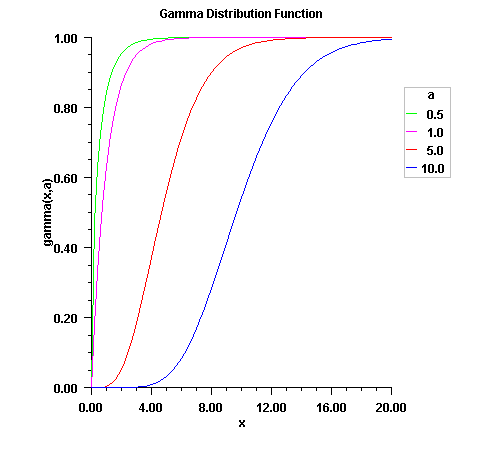
Gamma Distribution Function

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated.; a - a double scalar value representing the shape parameter. This must be positive.
Returns:: a double scalar value representing the probability that a gamma random variable takes on a value less than or equal to x.
See Also:: Example

gammaProb

public static double gammaProb(double x,
                               double a,
                               double b)

Evaluates the gamma probability density function.

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated.; a - a double scalar value representing the shape parameter. This must be positive.; b - a double scalar value representing the scale parameter. This must be positive.
Returns:: a double scalar value, the probability density function at x.

geometric

public static double geometric(int x,
                               double p)

Evaluates the discrete geometric cumulative probability distribution function.

Parameters:: x - an int scalar value representing the argument at which the function is to be evaluated; p - an double scalar value representing the probability parameter for each independent trial (the probability of success for each independent trial).
Returns:: a double scalar value representing the probability that a geometric random variable takes a value less than or equal to x. The return value is the probability that up to x trials would be observed before observing a success.

geometricProb

public static double geometricProb(int x,
                                   double p)

Evaluates the discrete geometric probability density function.

Method geometricProb evaluates the geometric distribution for the number of trials before the first success.

Parameters:: x - the int argument for which the geometric probability function is to be evaluated; p - a double scalar value representing the probability parameter of the geometric distribution (the probability of success for each independent trial)
Returns:: a double scalar value representing the probability that a geometric random variable takes a value equal to x.
See Also:: Example

hypergeometric

public static double hypergeometric(int k,
                                    int sampleSize,
                                    int defectivesInLot,
                                    int lotSize)

Evaluates the hypergeometric cumulative probability distribution function.

Method hypergeometric evaluates the distribution function of a hypergeometric random variable with parameters n, l, and m. The hypergeometric random variable X can be thought of as the number of items of a given type in a random sample of size n that is drawn without replacement from a population of size l containing m items of this type. The probability function is

$Pr left( {X = j} right) = frac{{left( {_j^m } right)left( {_{n - j}^{l - m} } right)}}{{left( {_n^l } right)}}{rm{for }},,j = i,;i + 1,,,i + 2,; ldots ,;min left( {n,m} right)$

where .

If k is greater than or equal to i and less than or equal to , hypergeometric sums the terms in this expression for j going from i up to k. Otherwise, hypergeometric returns 0 or 1, as appropriate. So, as to avoid rounding in the accumulation, hypergeometric performs the summation differently depending on whether or not k is greater than the mode of the distribution, which is the greatest integer less than or equal to .

Parameters:: k - an int, the argument at which the function is to be evaluated.; sampleSize - an int, the sample size, n.; defectivesInLot - an int, the number of defectives in the lot, m.; lotSize - an int, the lot size, l.
Returns:: a double, the probability that a hypergeometric random variable takes a value less than or equal to k.
See Also:: Example

hypergeometricProb

public static double hypergeometricProb(int k,
                                        int sampleSize,
                                        int defectivesInLot,
                                        int lotSize)

Evaluates the hypergeometric probability density function.

Method hypergeometricProb evaluates the probability density function of a hypergeometric random variable with parameters n, l, and m. The hypergeometric random variable X can be thought of as the number of items of a given type in a random sample of size n that is drawn without replacement from a population of size l containing m items of this type. The probability density function is:

${rm{Pr}}left( {X = k} right) = frac{{left( {_k^m } right)left( {_{n - k}^{l - m} } right)}}{{left( {_n^l } right)}}{rm{for}} ,,, k = i,;i + 1,,i + 2; ldots ,;min left( {n,m} right)$

where i = max(0, n - l + m). hypergeometricProb evaluates the expression using log gamma functions.

Parameters:: k - an int, the argument at which the function is to be evaluated.; sampleSize - an int, the sample size, n.; defectivesInLot - an int, the number of defectives in the lot, m.; lotSize - an int, the lot size, l.
Returns:: a double, the probability that a hypergeometric random variable takes on a value equal to k.
See Also:: Example

inverseBeta

public static double inverseBeta(double p,
                                 double pin,
                                 double qin)

Evaluates the inverse of the beta cumulative probability distribution function.

Method inverseBeta evaluates the inverse distribution function of a beta random variable with parameters pin and qin, that is, with P = p, p = pin, and q = qin, it determines x (equal to inverseBeta (p, pin, qin)), such that

$P = frac{{Gamma left( p right)Gamma left( q right)}}{{Gamma left( {p + q} right)}}int_0^x {t^{p - 1} } left( {1 - t} right)^{q - 1} dt$

where is the gamma function. The probability that the random variable takes a value less than or equal to x is P.

Parameters:: p - a double, the probability for which the inverse of the beta CDF is to be evaluated.; pin - a double, the first beta distribution parameter.; qin - a double, the second beta distribution parameter.
Returns:: a double, the probability that a beta random variable takes a value less than or equal to this returned value is p.
See Also:: Example

inverseChi

public static double inverseChi(double p,
                                double df)

Evaluates the inverse of the chi-squared cumulative probability distribution function.

Method inverseChi evaluates the inverse distribution function of a chi-squared random variable with df degrees of freedom, that is, with P = p and v = df, it determines x (equal to inverseChi(p, df)), such that

$P = frac{1}{{2^{nu /2} Gamma left( {nu /2} right)}}int_0^x {e^{ - t/2} t^{nu /2 - 1} } dt$

where is the gamma function. The probability that the random variable takes a value less than or equal to x is P.

For , inverseChi uses bisection, if or , or regula falsi to find the point at which the chi-squared distribution function is equal to P. The distribution function is evaluated using chi.

For , a modified Wilson-Hilferty approximation (Abramowitz and Stegun 1964, equation 26.4.18) to the normal distribution is used, and inverseNormal is used to evaluate the inverse of the normal distribution function. For , the ordinary Wilson-Hilferty approximation (Abramowitz and Stegun 1964, equation 26.4.17) is used.

Parameters:: p - a double scalar value representing the probability for which the inverse chi-squared function is to be evaluated.; df - a double scalar value representing the number of degrees of freedom. This must be at least 0.5.
Returns:: a double scalar value. The probability that a chi-squared random variable takes a value less than or equal to this returned value is p.
See Also:: Example

inverseDiscreteUniform

public static int inverseDiscreteUniform(double p,
                                         int n)

Returns the inverse of the discrete uniform cumulative probability distribution function.

Parameters:: p - a double scalar value representing the probability for which the inverse discrete uniform function is to be evaluated; n - an int scalar value representing the upper limit of the discrete uniform distribution
Returns:: a double scalar value. The probability that a discrete uniform random variable takes a value less than or equal to this returned value is p.

inverseExponential

public static double inverseExponential(double p,
                                        double scale)

Evaluates the inverse of the exponential cumulative probability distribution function.

Method inverseExponential evaluates the inverse distribution function of a gamma random variable with scale parameter =b and shape parameter a=1.0, that is, it determines , such that

$P = frac{1}{{Gamma left( a right)}}int_o^x {e^{ - t/b} } dt$

where is the gamma function. The probability that the random variable takes a value less than or equal to x is P. See the documentation for routine gamma for further discussion of the gamma distribution.

inverseExponential uses bisection and modified regula falsi to invert the distribution function, which is evaluated using method gamma.

Parameters:: p - a double scalar value representing the probability at which the function is to be evaluated.; scale - a double scalar value representing the scale parameter.
Returns:: a double scalar value. The probability that an exponential random variable takes a value less than or equal to this returned value is p.
See Also:: Example

inverseExtremeValue

public static double inverseExtremeValue(double p,
                                         double mu,
                                         double beta)

Returns the inverse of the extreme value cumulative probability distribution function.

Parameters:: p - a double scalar value representing the probability for which the inverse extreme value function is to be evaluated.; mu - a double scalar value representing the location parameter.; beta - a double scalar value representing the scale parameter.
Returns:: a double scalar value. The probability that an extreme value random variable takes a value less than or equal to this returned value is p.

inverseF

public static double inverseF(double p,
                              double dfn,
                              double dfd)

Returns the inverse of the F cumulative probability distribution function.

Method inverseF evaluates the inverse distribution function of a Snedecor's F random variable with dfn numerator degrees of freedom and dfd denominator degrees of freedom. The function is evaluated by making a transformation to a beta random variable and then using inverseBeta. If X is an F variate with and degrees of freedom and , then Y is a beta variate with parameters and . If , inverseF uses this relationship directly, otherwise, it also uses a relationship between X random variables that can be expressed as follows, using f, which is the F cumulative distribution function:

Parameters:: p - a double, the probability for which the inverse of the F distribution function is to be evaluated. Argument p must be in the open interval (0.0, 1.0).; dfn - a double, the numerator degrees of freedom. It must be positive.; dfd - a double, the denominator degrees of freedom. It must be positive.
Returns:: a double, the probability that an F random variable takes a value less than or equal to this returned value is p.
See Also:: Example

inverseGamma

public static double inverseGamma(double p,
                                  double a)

Evaluates the inverse of the gamma cumulative probability distribution function.

Method inverseGamma evaluates the inverse distribution function of a gamma random variable with shape parameter a, that is, it determines , such that

$P = frac{1}{{Gamma left( a right)}}int_o^x {e^{ - t} } t^{a - 1} dt$

inverseGamma uses bisection and modified regula falsi to invert the distribution function, which is evaluated using method gamma.

Parameters:: p - a double scalar value representing the probability at which the function is to be evaluated.; a - a double scalar value representing the shape parameter. This must be positive.
Returns:: a double scalar value. The probability that a gamma random variable takes a value less than or equal to this returned value is p.
See Also:: Example

inverseGeometric

public static double inverseGeometric(double r,
                                      double p)

Returns the inverse of the discrete geometric cumulative probability distribution function.

Parameters:: r - a double scalar value representing the probability for which the inverse geometric function is to be evaluated; p - an int scalar value representing the probability parameter for each independent trial (the probability of success for each independent trial).
Returns:: a double scalar value. The probability that a geometric random variable takes a value less than or equal to this returned value is r.

inverseLogNormal

public static double inverseLogNormal(double p,
                                      double mu,
                                      double sigma)

Returns the inverse of the standard lognormal cumulative probability distribution function.

Parameters:: p - a double scalar value representing the probability for which the inverse lognormal function is to be evaluated.; mu - a double scalar value representing the location parameter.; sigma - a double scalar value representing the shape parameter. sigma must be a positive.
Returns:: a double scalar value. The probability that a standard lognormal random variable takes a value less than or equal to this returned value is p.

inverseNoncentralchi

public static double inverseNoncentralchi(double p,
                                          double df,
                                          double alam)

Evaluates the inverse of the noncentral chi-squared cumulative probability distribution function.

Method inverseNoncentralchi evaluates the inverse distribution function of a noncentral chi-squared random variable with df degrees of freedom and noncentrality parameter alam, that is, with P = p, , and , it determines $c_{0} =$ inverseNoncentralchi(p, df, alam)), such that

$P = sumlimits_{i = 0}^infty {frac{e^{-lambda/2}left(lambda/2right)^i}{i!}} int_0^{c_{0}} {frac{x^{left(nu + 2iright)/2-1}e^{ - x/2}} {2^{left(nu+2iright)/2}{Gammaleft(frac{nu+2i}{2}right)}}} dx$

where is the gamma function. The probability that the random variable takes a value less than or equal to $c_{0}$ is .

Method inverseNoncentralchi uses bisection and modified regula falsi to invert the distribution function, which is evaluated using noncentralchi. See noncentralchi for an alternative definition of the noncentral chi-squared random variable in terms of normal random variables.

Parameters:: p - a double scalar value representing the probability for which the inverse noncentral chi-squared distribution function is to be evaluated. p must be in the open interval (0.0, 1.0).; df - a double scalar value representing the number of degrees of freedom. This must be at least 0.5. but less than or equal to 200,000.; alam - a double scalar value representing the noncentrality parameter. This must be nonnegative, and alam + df must be less than or equal to 200,000.
Returns:: a double scalar value. The probability that a noncentral chi-squared random variable takes a value less than or equal to this returned value is p.
See Also:: Example

inverseNoncentralstudentsT

public static double inverseNoncentralstudentsT(double p,
                                                int idf,
                                                double delta)

Evaluates the inverse of the noncentral Student's t cumulative probability distribution function.

Method inverseNoncentralstudentsT evaluates the inverse distribution function of a noncentral t random variable with idf degrees of freedom and noncentrality parameter delta; that is, with , , , it determines $t_{0} =$ inverseNoncentralstudentsT(p, idf, delta)), such that

$P = int_{-{infty}}^{t_{0}}{frac{nu^{nu/2}e^{{-delta^2}/2}} {{sqrt{pi}Gammaleft(nu/2right)left(nu+x^2right)}^{left(nu+1right)/2}} } sumlimits_{i = 0}^infty {Gammaleft(left(nu+i+1right)/2right)left(frac{delta^i}{i!}right) left(frac{2x^2}{nu+x^2}right)^{i/2} dx}$

where is the gamma function. The probability that the random variable takes a value less than or equal to $t_{0}$ is P. See noncentralstudentsT for an alternative definition in terms of normal and chi-squared random variables. The method inverseNoncentralstudentsT uses bisection and modified regula falsi to invert the distribution function, which is evaluated using noncentralstudentsT.

Parameters:: p - a double scalar value representing the probability for which the function is to be evaluated.; idf - an int scalar value representing the number of degrees of freedom. This must be positive.; delta - a double scalar value representing the noncentrality parameter.
Returns:: a double scalar value. The probability that a noncentral Student's t random variable takes a value less than or equal to this returned value is p.
See Also:: Example

inverseNormal

public static double inverseNormal(double p)

Evaluates the inverse of the normal (Gaussian) cumulative probability distribution function.

Method inverseNormal evaluates the inverse of the distribution function, , of a standard normal (Gaussian) random variable, that is, inverseNormal , where

$Phi left( x right) = frac{1}{{sqrt {2pi } }}int_{ - infty }^x {e^{ - t^2 /2} dt}$

The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x. The standard normal distribution has a mean of 0 and a variance of 1.

Parameters:: p - a double scalar value representing the probability at which the function is to be evaluated.
Returns:: a double scalar value. The probability that a standard normal random variable takes a value less than or equal to this returned value is p.
See Also:: Example

inverseRayleigh

public static double inverseRayleigh(double p,
                                     double alpha)

Returns the inverse of the Rayleigh cumulative probability distribution function.

Parameters:: p - a double scalar value representing the probability for which the inverse Rayleigh function is to be evaluated.; alpha - a double scalar value representing the scale parameter.
Returns:: a double scalar value. The probability that a Rayleigh random variable takes a value less than or equal to this returned value is p.

inverseStudentsT

public static double inverseStudentsT(double p,
                                      double df)

Returns the inverse of the Student's t cumulative probability distribution function.

inverseStudentsT evaluates the inverse distribution function of a Student's t random variable with df degrees of freedom. Let v = df. If v equals 1 or 2, the inverse can be obtained in closed form, if v is between 1 and 2, the relationship of a t to a beta random variable is exploited and inverseBeta is used to evaluate the inverse; otherwise the algorithm of Hill (1970) is used. For small values of v greater than 2, Hill's algorithm inverts an integrated expansion in of the t density. For larger values, an asymptotic inverse Cornish-Fisher type expansion about normal deviates is used.

Parameters:: p - a double scalar value representing the probability for which the inverse Student's t function is to be evaluated.; df - a double scalar value representing the number of degrees of freedom. This must be at least one.
Returns:: a double scalar value. The probability that a Student's t random variable takes a value less than or equal to this returned value is p.
See Also:: Example

inverseUniform

public static double inverseUniform(double p,
                                    double aa,
                                    double bb)

Returns the inverse of the uniform cumulative probability distribution function.

Parameters:: p - a double scalar value representing the probability for which the inverse uniform function is to be evaluated.; aa - a double scalar value representing the minimum value.; bb - a double scalar value representing the maximum value.
Returns:: a double scalar value. The probability that a uniform random variable takes a value less than or equal to this returned value is p.

inverseWeibull

public static double inverseWeibull(double p,
                                    double gamma,
                                    double alpha)

Returns the inverse of the Weibull cumulative probability distribution function.

Parameters:: p - a double scalar value representing the probability for which the inverse Weibull function is to be evaluated.; gamma - a double scalar value representing the shape parameter.; alpha - a double scalar value representing the scale parameter.
Returns:: a double scalar value. The probability that a Weibull random variable takes a value less than or equal to this returned value is p.

logNormal

public static double logNormal(double x,
                               double mu,
                               double sigma)

Evaluates the standard lognormal cumulative probability distribution function.

$Fleft( x right) = frac{1}{x^{sigma}sqrt{2pi}} int{frac{1}{t}e^{-frac{ {ln{t}-mu}^2 }{2{sigma}^2}} }$

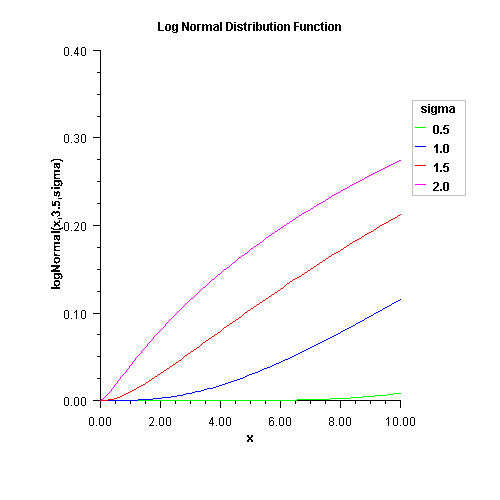
Plot of Lognormal Distribution Function

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated.; mu - a double scalar value representing the location parameter.; sigma - a double scalar value representing the shape parameter. sigma must be a positive.
Returns:: a double scalar value representing the probability that a standard lognormal random variable takes a value less than or equal to x.

logNormalProb

public static double logNormalProb(double x,
                                   double mu,
                                   double sigma)

Evaluates the standard lognormal probability density function.

$Fleft( x right) = frac{1}{x^{sigma}sqrt{2pi}} {e^{-frac{ {(ln{x}-mu)}^2 }{2{sigma}^2}} }$

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated.; mu - a double scalar value representing the scale parameter.; sigma - a double scalar value representing the shape parameter. sigma must be a positive.
Returns:: a double scalar value representing the probability density function at x.

noncentralchi

public static double noncentralchi(double chsq,
                                   double df,
                                   double alam)

Evaluates the noncentral chi-squared cumulative probability distribution function.

Method noncentralchi evaluates the distribution function, F, of a noncentral chi-squared random variable with df degrees of freedom and noncentrality parameter alam, that is, with , , and ,

$Fleft( x right) = sumlimits_{i = 0}^infty {frac{e^{-lambda/2}left(lambda/2right)^i}{i!}} int_0^x {frac{t^{left(nu + 2iright)/2-1}e^{ - t/2}} {2^{left(nu+2iright)/2}{Gammaleft(frac{nu+2i}{2}right)}}} dt$

where is the gamma function. This is a series of central chi-squared distribution functions with Poisson weights. The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.

The noncentral chi-squared random variable can be defined by the distribution function above, or alternatively and equivalently, as the sum of squares of independent normal random variables. If the have independent normal distributions with means ${mu}_i$ and variances equal to one and

$X = sumlimits_{i = 1}^n{Y_i}^2$

then has a noncentral chi-squared distribution with degrees of freedom and noncentrality parameter equal to

$sumlimits_{i = 1}^n{mu_i}^2$

With a noncentrality parameter of zero, the noncentral chi-squared distribution is the same as the chi-squared distribution.

noncentralchi determines the point at which the Poisson weight is greatest, and then sums forward and backward from that point, terminating when the additional terms are sufficiently small or when a maximum of 1000 terms have been accumulated. The recurrence relation 26.4.8 of Abramowitz and Stegun (1964) is used to speed the evaluation of the central chi-squared distribution functions.

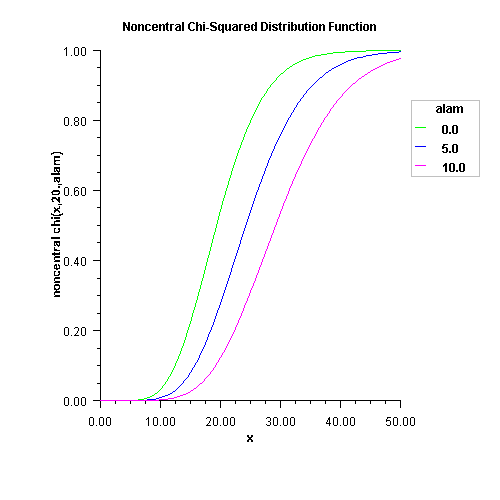
Noncentral Chi-Squared Distribution Function

Parameters:: chsq - a double scalar value representing the argument at which the function is to be evaluated.; df - a double scalar value representing the number of degrees of freedom. This must be at least 0.5.; alam - a double scalar value representing the noncentrality parameter. This must be nonnegative, and alam + df must be less than or equal to 200,000.
Returns:: a double scalar value representing the probability that a chi-squared random variable takes a value less than or equal to chsq.
See Also:: Example

noncentralstudentsT

public static double noncentralstudentsT(double t,
                                         int idf,
                                         double delta)

Evaluates the noncentral Student's t cumulative probability distribution function.

Method noncentralstudentsT evaluates the distribution function F of a noncentral t random variable with idf degrees of freedom and noncentrality parameter delta; that is, with , , and $t_{0}= t$ ,

$F{left({t_0}right)} = int_{-{infty}}^{t_{0}} {frac {nu^{nu/2}e^{{-delta^2}/2}} {{sqrt{pi}Gammaleft(nu/2right)left(nu+x^2right)}^{left(nu+1right)/2}} } sumlimits_{i = 0}^infty {Gammaleft(left(nu+i+1right)/2right)left(frac{delta^i}{i!}right)left(frac{2x^2}{nu+x^2}right)^{i/2} dx }$

where is the gamma function. The value of the distribution function at the point $t_{0}$ is the probability that the random variable takes a value less than or equal to $t_{0}$ .

The noncentral t random variable can be defined by the distribution function above, or alternatively and equivalently, as the ratio of a normal random variable and an independent chi-squared random variable. If w has a normal distribution with mean and variance equal to one, has an independent chi-squared distribution with degrees of freedom, and

then has a noncentral distribution with degrees of freedom and noncentrality parameter .

The distribution function of the noncentral can also be expressed as a double integral involving a normal density function (see, for example, Owen 1962, page 108). The method noncentralstudentsT uses the method of Owen (1962, 1965), which uses repeated integration by parts on that alternate expression for the distribution function.

Noncentral Student's t Distribution Function

Parameters:: t - a double scalar value representing the argument at which the function is to be evaluated.; idf - an int scalar value representing the number of degrees of freedom. This must be positive.; delta - a double scalar value representing the noncentrality parameter.
Returns:: a double scalar value representing the probability that a noncentral Student's t random variable takes a value less than or equal to t.
See Also:: Example

normal

public static double normal(double x)

Evaluates the normal (Gaussian) cumulative probability distribution function.

Method normal evaluates the distribution function, , of a standard normal (Gaussian) random variable, that is,

$Phi left( x right) = frac{1}{{sqrt {2pi } }}int_{ - infty }^x {} e^{ - t^2 /2} dt$

The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.

The standard normal distribution (for which normal is the distribution function) has mean of 0 and variance of 1. The probability that a normal random variable with mean and variance is less than y is given by normal evaluated at .

is evaluated by use of the complementary error function, erfc. The relationship is:

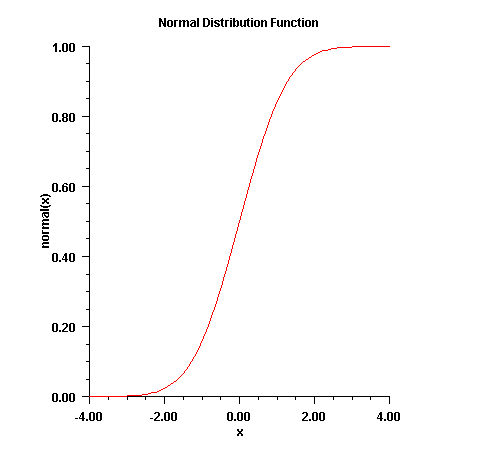
Standard Normal Distribution Function

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated.
Returns:: a double scalar value representing the probability that a normal variable takes a value less than or equal to x.
See Also:: Example

poisson

public static double poisson(int k,
                             double theta)

Evaluates the Poisson cumulative probability distribution function.

poisson evaluates the distribution function of a Poisson random variable with parameter theta. theta, which is the mean of the Poisson random variable, must be positive. The probability function (with ) is

$f(x) = e^{ - theta } theta ^x /x!,,, for,x = 0,,1,,2,, ldots$

The individual terms are calculated from the tails of the distribution to the mode of the distribution and summed. poisson uses the recursive relationship

with $f(0) = e^{-theta}$ .

Parameters:: k - the int argument for which the Poisson distribution function is to be evaluated.; theta - a double scalar value representing the mean of the Poisson distribution.
Returns:: a double scalar value representing the probability that a Poisson random variable takes a value less than or equal to k.
See Also:: Example

poissonProb

public static double poissonProb(int k,
                                 double theta)

Evaluates the Poisson probability density function.

Method poissonProb evaluates the probability density function of a Poisson random variable with parameter theta. theta, which is the mean of the Poisson random variable, must be positive. The probability function (with ) is

$f(x) = e^{- theta} ,,theta ^k /k!,,,,,, for,k = 0,,,1,,,2,, ldots$

poissonProb evaluates this function directly, taking logarithms and using the log gamma function.

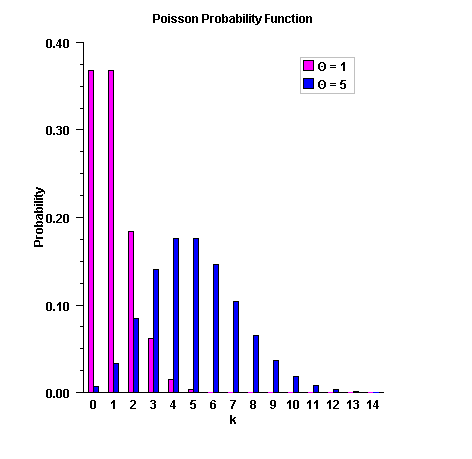
Poisson ProbabilityFunction

Parameters:: k - the int argument for which the Poisson probability function is to be evaluated.; theta - a double scalar value representing the mean of the Poisson distribution.
Returns:: a double scalar value representing the probability that a Poisson random variable takes a value equal to k.
See Also:: Example

Rayleigh

public static double Rayleigh(double x,
                              double alpha)

Evaluates the Rayleigh cumulative probability distribution function.

Method Rayleigh is a special case of Weibull distribution function where the shape parameter gamma is 2.0; that is,

$F(x) = 1-e^{-frac{x^2}{2alpha^2}}$

where alpha is the scale parameter.

Plot of Rayleigh Distribution Function

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated. It must be non-negative.; alpha - a double scalar value representing the scale parameter.
Returns:: a double scalar value representing the probability that a Rayleigh random variable takes a value less than or equal to x.

RayleighProb

public static double RayleighProb(double x,
                                  double alpha)

Evaluates the Rayleigh probability density function.

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated. It must be non-negative.; alpha - a double scalar value representing the scale parameter.
Returns:: a double scalar value representing the probability density function at x.

studentsT

public static double studentsT(double t,
                               double df)

Evaluates the Student's t cumulative probability distribution function.

Method studentsT evaluates the distribution function of a Student's t random variable with df degrees of freedom. If the square of t is greater than or equal to df, the relationship of a t to an f random variable (and subsequently, to a beta random variable) is exploited, and routine beta is used. Otherwise, the method described by Hill (1970) is used. If df is not an integer, if df is greater than 19, or if df is greater than 200, a Cornish-Fisher expansion is used to evaluate the distribution function. If df is less than 20 and is less than 2.0, a trigonometric series (see Abramowitz and Stegun 1964, equations 26.7.3 and 26.7.4, with some rearrangement) is used. For the remaining cases, a series given by Hill (1970) that converges well for large values of t is used.

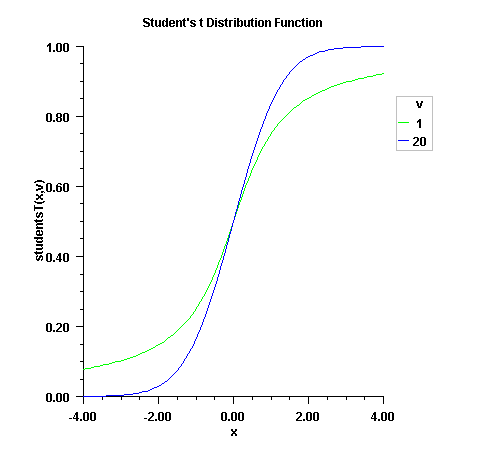
Student's t Distribution Function

Parameters:: t - a double scalar value representing the argument at which the function is to be evaluated; df - a double scalar value representing the number of degrees of freedom. This must be at least one.
Returns:: a double scalar value representing the probability that a Student's t random variable takes a value less than or equal to t.
See Also:: Example

uniform

public static double uniform(double x,
                             double aa,
                             double bb)

Evaluates the uniform cumulative probability distribution function.

Method uniform evaluates the distribution function, F, of a uniform random variable with location parameter aa and scale parameter bb; that is,

$f(x)=left{begin{array}{cc}0,&mbox{if }x lt aa\frac{x-aa}{bb-aa},&mbox{if }aale xle bb\1,&mbox{if }x>bb end{array}right.$

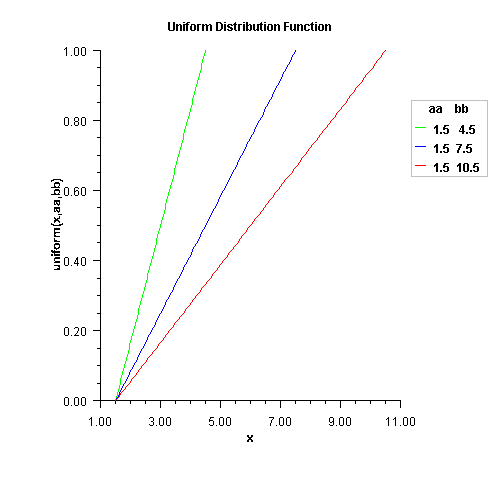
Plot of Uniform Distribution Function

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated.; aa - a double scalar value representing the location parameter.; bb - a double scalar value representing the scale parameter.
Returns:: a double scalar value representing the probability that a uniform random variable takes a value less than or equal to x.

Weibull

public static double Weibull(double x,
                             double gamma,
                             double alpha)

Evaluates the Weibull cumulative probability distribution function.

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated. It must be non-negative.; gamma - a double scalar value representing the shape parameter.; alpha - a double scalar value representing the scale parameter.
Returns:: a double scalar value representing the probability that a Weibull random variable takes a value less than or equal to x.

WeibullProb

public static double WeibullProb(double x,
                                 double gamma,
                                 double alpha)

Evaluates the Weibull probability density function.

Parameters:: x - a double scalar value representing the argument at which the function is to be evaluated. It must be non-negative.; gamma - a double scalar value representing the shape parameter.; alpha - a double scalar value representing the scale parameter.
Returns:: a double scalar value, the probability density function at x.