 com.imsl.stat.CrossCorrelation
com.imsl.stat.CrossCorrelation
|
JMSLTM Numerical Library 4.0 | ||||||||
| PREV CLASS NEXT CLASS | FRAMES NO FRAMES | ||||||||
| SUMMARY: NESTED | FIELD | CONSTR | METHOD | DETAIL: FIELD | CONSTR | METHOD | ||||||||
java.lang.Objectcom.imsl.stat.CrossCorrelation
Computes the sample cross-correlation function of two stationary time series.
CrossCorrelation estimates the cross-correlation function of
two jointly stationary time series given a sample of n =
x.length observations ![]() and
and ![]() for t = 1,2, ..., n.
for t = 1,2, ..., n.
Let
![]()
![]()
The autocovariance function of ![]() ,
,
![]() , is estimated by
, is estimated by
![]()
maximum_lag. Note that
x returned by method
getVarianceX. The autocorrelation function
![]()
Note that ![]() by definition.
Let
by definition.
Let
![]()
The cross-covariance function ![]() is
estimated by
is
estimated by
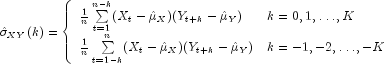
![]()
The standard errors of the sample cross-correlations may be optionally
computed according to the getStandardErrors method argument
stderrMethod. One method is based on a general
asymptotic expression for the variance of the sample cross-correlation
coefficient of two jointly stationary time series with independent,
identically distributed normal errors given by Bartlet (1978, page 352).
The theoretical formula is
![begin{array}{c}
{rm var} left { hat rho _{XY}(k) right } =
frac{1}{n-k}sumlimits_{i=-infty}^{infty}
left [right. {rho _X(i)}+rho _{XY}(i-k)rho _{XY}(i+k) \
-2rho _{XY}(k){rho _X(i)rho _{XY}(i+k)+rho _{XY}(-i)rho _Y(i+k)} \
+rho^2_{XY}(k){rho_X(i) + frac{1}{2}rho^2_X(i) +
frac{1}{2}rho^2_Y(i)} left. right ] end{array}](eqn_1733.png)
A second method evaluates Bartlett's formula under the additional assumption that the two series have no cross-correlation. The theoretical formula is
![]()
An important property of the cross-covariance coefficient is
![]() for
for
![]() . This result is used in the computation
of the standard error of the sample cross-correlation for lag
. This result is used in the computation
of the standard error of the sample cross-correlation for lag ![]() .
In general, the cross-covariance function is not symmetric about zero
so both positive and negative lags are of interest.
.
In general, the cross-covariance function is not symmetric about zero
so both positive and negative lags are of interest.
| Nested Class Summary | |
static class |
CrossCorrelation.NonPosVariancesException
The problem is ill-conditioned. |
| Field Summary | |
static int |
BARTLETTS_FORMULA
Indicates standard error computation using Bartlett's formula. |
static int |
BARTLETTS_FORMULA_NOCC
Indicates standard error computation using Bartlett's formula with the assumption of no cross-correlation. |
| Constructor Summary | |
CrossCorrelation(double[] x,
double[] y,
int maximum_lag)
Constructor to compute the sample cross-correlation function of two stationary time series. |
|
| Method Summary | |
double[] |
getAutoCorrelationX()
Returns the autocorrelations of the time series x. |
double[] |
getAutoCorrelationY()
Returns the autocorrelations of the time series y. |
double[] |
getAutoCovarianceX()
Returns the autocovariances of the time series x. |
double[] |
getAutoCovarianceY()
Returns the autocovariances of the time series y. |
double[] |
getCrossCorrelation()
Returns the cross-correlations between the time series x
and y. |
double[] |
getCrossCovariance()
Returns the cross-covariances between the time series x
and y. |
double |
getMeanX()
Returns the mean of the time series x. |
double |
getMeanY()
Returns the mean of the time series y. |
double[] |
getStandardErrors(int stderrMethod)
Returns the standard errors of the cross-correlations between the time series x and y. |
double |
getVarianceX()
Returns the variance of time series x. |
double |
getVarianceY()
Returns the variance of time series y. |
void |
setMeanX(double mean)
Estimate of the mean of time series x. |
void |
setMeanY(double mean)
Estimate of the mean of time series y. |
| Methods inherited from class java.lang.Object |
clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait |
| Field Detail |
public static final int BARTLETTS_FORMULA
public static final int BARTLETTS_FORMULA_NOCC
| Constructor Detail |
public CrossCorrelation(double[] x,
double[] y,
int maximum_lag)
x - A one-dimensional double
array containing the first stationary
time series.y - A one-dimensional double
array containing the second stationary
time series.maximum_lag - An int containing
the maximum lag of the cross-covariance and
cross-correlations to be computed.
maximum_lag must be greater
than or equal to 1 and less than the minimum
of the number of observations of x
and y.| Method Detail |
public double[] getAutoCorrelationX()
throws CrossCorrelation.NonPosVariancesException
x.
double array of length maximum_lag +1
containing the autocorrelations of the time series x.
The 0-th element of this array is 1. The k-th element of this array
contains the autocorrelation of lag k where
k = 1, ..., maximum_lag.
CrossCorrelation.NonPosVariancesException
public double[] getAutoCorrelationY()
throws CrossCorrelation.NonPosVariancesException
y.
double array of length maximum_lag +1
containing the autocorrelations of the time series y.
The 0-th element of this array is 1. The k-th element of this array
contains the autocorrelation of lag k where
k = 1, ..., maximum_lag.
CrossCorrelation.NonPosVariancesException
public double[] getAutoCovarianceX()
throws CrossCorrelation.NonPosVariancesException
x.
double array of length maximum_lag +1
containing the variances and autocovariances of the time series x.
The 0-th element of the array contains the variance of the time series
x. The k-th element contains the autocovariance of lag k
where k = 1, ..., maximum_lag.
CrossCorrelation.NonPosVariancesException
public double[] getAutoCovarianceY()
throws CrossCorrelation.NonPosVariancesException
y.
double array of length maximum_lag +1
containing the variances and autocovariances of the time series y.
The 0-th element of the array contains the variance of the time series
x. The k-th element contains the autocovariance of lag k
where k = 1, ..., maximum_lag.
CrossCorrelation.NonPosVariancesException
public double[] getCrossCorrelation()
throws CrossCorrelation.NonPosVariancesException
x
and y.
double array of length 2 * maximum_lag +1
containing the cross-correlations between the time series x
and y. The cross-correlation between x and
y at lag k, where k = -maximum_lag
,..., 0, 1,...,maximum_lag, corresponds to output array indices
0, 1,..., (2*maximum_lag).
CrossCorrelation.NonPosVariancesExceptionpublic double[] getCrossCovariance()
x
and y.
double array of length 2 * maximum_lag +1
containing the cross-covariances between the time series x
and y. The cross-covariance between x and
y at lag k, where k = -maximum_lag
,..., 0, 1,...,maximum_lag, corresponds to output array indices
0, 1,..., (2*maximum_lag).public double getMeanX()
x.
double containing the mean
of the time series x.public double getMeanY()
y.
double containing the mean
of the time series y.
public double[] getStandardErrors(int stderrMethod)
throws CrossCorrelation.NonPosVariancesException
x and y. Method of computation for
standard errors of the cross-correlation is determined by the
stderrMethod parameter. If stderrMethod
is set to BARTLETTS_FORMULA, Bartlett's formula is used to compute the
standard errors of cross-correlations. If
stderrMethod is set to BARTLETTS_FORMULA_NOCC, Bartlett's
formula is used to compute the standard errors of
cross-correlations, with the assumption of no cross-correlation.
stderrMethod - An int specifying the
method to compute the standard errors of
cross-correlations between the time series x
and y.
double array of length 2 * maximum_lag + 1
containing the standard errors of the cross-correlations between the
time series x and y. The standard error of
cross-correlations between x and y at lag
k, where k = -maximum_lag,..., 0, 1,...,
maximum_lag, corresponds to output array indices
0, 1,..., (2*maximum_lag).
CrossCorrelation.NonPosVariancesException
public double getVarianceX()
throws CrossCorrelation.NonPosVariancesException
x.
double containing the variance
of the time series x.
CrossCorrelation.NonPosVariancesException
public double getVarianceY()
throws CrossCorrelation.NonPosVariancesException
y.
double containing the variance
of the time series y.
CrossCorrelation.NonPosVariancesExceptionpublic void setMeanX(double mean)
x.
mean - A double containing the
estimate mean of the time series x.public void setMeanY(double mean)
y.
mean - A double containing the
estimate mean of the time series y.
|
JMSLTM Numerical Library 4.0 | ||||||||
| PREV CLASS NEXT CLASS | FRAMES NO FRAMES | ||||||||
| SUMMARY: NESTED | FIELD | CONSTR | METHOD | DETAIL: FIELD | CONSTR | METHOD | ||||||||