 com.imsl.stat.ARMA
com.imsl.stat.ARMA
|
JMSLTM Numerical Library 4.0 | ||||||||
| PREV CLASS NEXT CLASS | FRAMES NO FRAMES | ||||||||
| SUMMARY: NESTED | FIELD | CONSTR | METHOD | DETAIL: FIELD | CONSTR | METHOD | ||||||||
java.lang.Objectcom.imsl.stat.ARMA
Computes least-square estimates of parameters for an ARMA model.
Class ARMA computes estimates of parameters for a
nonseasonal ARMA model given a sample of observations,
![]() , for
, for ![]() ,
where n =
,
where n = z.length.
Two methods of parameter estimation, method of moments and least squares,
are provided. The user can choose a method using the setMethod
method. If the user wishes to use the least-squares algorithm, the
preliminary estimates are the method of moments estimates by default.
Otherwise, the user can input initial estimates by using the
setInitialEstimates method. The following table lists the appropriate
methods for both the method of moments and least-squares algorithm:
| Least Squares | Both Method of Moment and Least Squares |
setCenter |
|
setARLags |
setMethod |
setMALags |
setRelativeError |
setBackcasting |
setMaxIterations |
setConvergenceTolerance |
setMeanEstimate |
setInitialEstimates |
getMeanEstimate |
getResidual |
getAutocovariance |
getSSResidual |
getVariance |
getParamEstimatesCovariance |
getConstant |
getAR |
|
getMA |
Method of Moments Estimation
Suppose the time series ![]() is generated by an
ARMA (p, q) model of the form
is generated by an
ARMA (p, q) model of the form
![]()
![]()
Let ![]() be the estimate of the
mean
be the estimate of the
mean ![]() of the time series
of the time series ![]() ,
where
,
where ![]() equals the following:
equals the following:
![]()
The autocovariance function is estimated by
![]()
for ![]() , where
K = p + q. Note that
, where
K = p + q. Note that ![]() is an estimate of the sample variance.
is an estimate of the sample variance.
Given the sample autocovariances, the function computes the method of moments estimates of the autoregressive parameters using the extended Yule-Walker equations as follows:
![]()
where
![]()
![]()
![]()
The overall constant ![]() is estimated by
the following:
is estimated by
the following:
![]()
The moving average parameters are estimated based on a system of
nonlinear equations given K = p + q + 1 autocovariances,
![]() , and
p autoregressive parameters
, and
p autoregressive parameters ![]() for
for
![]() .
.
Let ![]() . The autocovariances of the
derived moving average process
. The autocovariances of the
derived moving average process ![]() are
estimated by the following relation:
are
estimated by the following relation:
![]()
The iterative procedure for determining the moving average parameters is based on the relation
![]()
where ![]() denotes the autocovariance
function of the original
denotes the autocovariance
function of the original ![]() process.
process.
Let ![]() and
and
![]() , where
, where
![]()
and
![]()
Then, the value of ![]() at the (i + 1)-th iteration
is determined by the following:
at the (i + 1)-th iteration
is determined by the following:
![]()
The estimation procedure begins with the initial value
![]()
and terminates at iteration i when either ![]() is less than
is less than relativeError or i
equals iterations. The moving average parameter estimates are
obtained from the final estimate of ![]() by setting
by setting
![]()
The random shock variance is estimated by the following:
![]()
See Box and Jenkins (1976, pp. 498-500) for a description of a function that performs similar computations.
Least-squares Estimation
Suppose the time series ![]() is generated by a
nonseasonal ARMA model of the form,
is generated by a
nonseasonal ARMA model of the form,
![]()
where B is the backward shift operator, ![]() is the mean of
is the mean of ![]() , and
, and
![]()
![]()
with p autoregressive and q moving average parameters. Without loss of generality, the following is assumed:
![]()
![]()
so that the nonseasonal ARMA model is of order
![]() , where
, where ![]() and
and ![]() . Note that the usual hierarchical
model assumes the following:
. Note that the usual hierarchical
model assumes the following:
![]()
![]()
Consider the sum-of-squares function
![]()
where
![]()
and T is the backward origin. The random shocks
![]() are assumed to be independent and identically
distributed
are assumed to be independent and identically
distributed
![]()
random variables. Hence, the log-likelihood function is given by
![]()
where ![]() is a function of
is a function of
![]() .
.
For T = 0, the log-likelihood function is
conditional on the past values of both ![]() and
and
![]() required to initialize the model. The method of
selecting these initial values usually introduces transient bias into the
model (Box and Jenkins 1976, pp. 210-211). For
required to initialize the model. The method of
selecting these initial values usually introduces transient bias into the
model (Box and Jenkins 1976, pp. 210-211). For ![]() ,
this dependency vanishes, and estimation problem concerns maximization of
the unconditional log-likelihood function. Box and Jenkins (1976, p. 213)
argue that
,
this dependency vanishes, and estimation problem concerns maximization of
the unconditional log-likelihood function. Box and Jenkins (1976, p. 213)
argue that
![]()
dominates
![]()
The parameter estimates that minimize the sum-of-squares function are called least-squares estimates. For large n, the unconditional least-squares estimates are approximately equal to the maximum likelihood-estimates.
In practice, a finite value of T will enable sufficient
approximation of the unconditional sum-of-squares function. The values of
![]() needed to compute the unconditional sum of
squares are computed iteratively with initial values of
needed to compute the unconditional sum of
squares are computed iteratively with initial values of ![]() obtained by back forecasting. The residuals (including backcasts), estimate
of random shock variance, and covariance matrix of the final parameter
estimates also are computed. ARIMA parameters can be computed by using
obtained by back forecasting. The residuals (including backcasts), estimate
of random shock variance, and covariance matrix of the final parameter
estimates also are computed. ARIMA parameters can be computed by using
Difference with ARMA.
Forecasting
The Box-Jenkins forecasts and their associated probability limits for a
nonseasonal ARMA model are computed given a sample of
n = z.length, ![]() for
for ![]() .
.
Suppose the time series ![]() is generated by a
nonseasonal ARMA model of the form
is generated by a
nonseasonal ARMA model of the form
![]()
for ![]() ,
where B is the backward shift operator,
,
where B is the backward shift operator, ![]() is the constant, and
is the constant, and
![]()
![]()
with p autoregressive and q moving average parameters. Without loss of generality, the following is assumed:
![]()
![]()
so that the nonseasonal ARMA model is of order
![]() , where
, where ![]() and
and ![]() . Note that the usual hierarchical
model assumes the following:
. Note that the usual hierarchical
model assumes the following:
![]()
![]()
The Box-Jenkins forecast at origin t for lead time l of
![]() is defined in terms of the difference equation
is defined in terms of the difference equation
![]()
![]()
where the following is true:
![]()
![]()
The ![]() percent probability limits for
percent probability limits for
![]() are given by
are given by
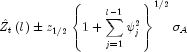
where ![]() is the
is the
![]() percentile of the standard normal
distribution
percentile of the standard normal
distribution
![]()
and
![]()
are the parameters of the random shock form of the difference equation.
Note that the forecasts are computed for lead times
![]() at origins
at origins
![]() , where
, where
![]() and
and
![]() .
.
The Box-Jenkins forecasts minimize the mean-square error
![]()
Also, the forecasts can be easily updated according to the following equation:
![]()
This approach and others are discussed in Chapter 5 of Box and Jenkins (1976).
| Nested Class Summary | |
static class |
ARMA.IllConditionedException
The problem is ill-conditioned. |
static class |
ARMA.IncreaseErrRelException
The bound for the relative error is too small. |
static class |
ARMA.MatrixSingularException
The input matrix is singular. |
static class |
ARMA.NewInitialGuessException
The iteration has not made good progress. |
static class |
ARMA.TooManyCallsException
The number of calls to the function has exceeded the maximum number of iterations. |
static class |
ARMA.TooManyFcnEvalException
Maximum number of function evaluations exceeded. |
static class |
ARMA.TooManyITNException
Maximum number of iterations exceeded. |
static class |
ARMA.TooManyJacobianEvalException
Maximum number of Jacobian evaluations exceeded. |
| Field Summary | |
static int |
LEAST_SQUARES
Indicates autoregressive and moving average parameters are estimated by a least-squares procedure. |
static int |
METHOD_OF_MOMENTS
Indicates autoregressive and moving average parameters are estimated by a method of moments procedure. |
| Constructor Summary | |
ARMA(int p,
int q,
double[] z)
Constructor for ARMA. |
|
| Method Summary | |
void |
compute()
Computes least-square estimates of parameters for an ARMA model. |
double[][] |
forecast(int nPredict)
Computes forecasts and their associated probability limits for an ARMA model. |
double[] |
getAR()
Returns the final autoregressive parameter estimates. |
double[] |
getAutoCovariance()
Returns the autocovariances of the time series z. |
double |
getConstant()
Returns the constant parameter estimate. |
double[] |
getDeviations()
Returns the deviations from each forecast that give the confidence percent probability limits. |
double[] |
getMA()
Returns the final moving average parameter estimates. |
double |
getMeanEstimate()
Returns an update of the mean of the time series z. |
double[][] |
getParamEstimatesCovariance()
Returns the covariances of parameter estimates. |
double[] |
getPsiWeights()
Returns the psi weights of the infinite order moving average form of the model. |
double[] |
getResidual()
Returns the residuals. |
double |
getSSResidual()
Returns the sum of squares of the random shock. |
double |
getVariance()
Returns the variance of the time series z. |
void |
setARLags(int[] arLags)
Sets the order of the autoregressive parameters. |
void |
setBackcasting(int length,
double tolerance)
Sets backcasting option. |
void |
setBackwardOrigin(int backwardOrigin)
Sets the maximum backward origin. |
void |
setCenter(boolean center)
Sets center option. |
void |
setConfidence(double confidence)
Sets the confidence percent probability limits of the forecasts. |
void |
setConvergenceTolerance(double convergenceTolerance)
Sets the tolerance level used to determine convergence of the nonlinear least-squares algorithm. |
void |
setInitialEstimates(double[] ar,
double[] ma)
Sets preliminary estimates. |
void |
setMALags(int[] maLags)
Sets the order of the moving average parameters. |
void |
setMaxIterations(int iterations)
Sets the maximum number of iterations. |
void |
setMeanEstimate(double zMean)
Sets an initial estimate of the mean of the time series z. |
void |
setMethod(int method)
Sets the method to be used by the class. |
void |
setRelativeError(double relativeError)
Sets the stopping criterion for use in the nonlinear equation solver. |
| Methods inherited from class java.lang.Object |
clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait |
| Field Detail |
public static final int LEAST_SQUARES
public static final int METHOD_OF_MOMENTS
| Constructor Detail |
public ARMA(int p,
int q,
double[] z)
ARMA.
p - an int scalar containing the number of
autoregressive (AR) parametersq - an int scalar containing the number of moving
average (MA) parametersz - a double array containing the observations
IllegalArgumentException - is thrown if p,
q, and z.length are not
consistent.| Method Detail |
public final void compute()
throws ARMA.MatrixSingularException,
ARMA.TooManyCallsException,
ARMA.IncreaseErrRelException,
ARMA.NewInitialGuessException,
ARMA.IllConditionedException,
ARMA.TooManyITNException,
ARMA.TooManyFcnEvalException,
ARMA.TooManyJacobianEvalException
ARMA.MatrixSingularException - is thrown if the input matrix is
singular
ARMA.TooManyCallsException - is thrown if the number of calls to
the function has exceeded
ARMA.IncreaseErrRelException - is thrown if the bound for the
relative error is too small
ARMA.NewInitialGuessException - is thrown if the iteration has not
made good progress
ARMA.IllConditionedException - is thrown if the problem is
ill-conditioned
ARMA.TooManyITNException - is thrown if the maximum number of
iterations exceeded
ARMA.TooManyFcnEvalException - is thrown if the maximum number of
function evaluations exceeded
ARMA.TooManyJacobianEvalException - is thrown if the maximum number
of Jacobian evaluations exceededpublic final double[][] forecast(int nPredict)
nPredict - an int scalar containing the maximum
lead time for forecasts. nPredict
must be greater than 0.
double matrix of dimensions of
nPredict by backwardOrigin + 1
containing the forecasts. Return NULL if the
least-square estimates of parameters is not computed.public double[] getAR()
double array of length p containing
the final autoregressive parameter estimatespublic double[] getAutoCovariance()
z.
double array containing the autocovariances of
lag k, where k = 1, ..., p + q + 1public double getConstant()
double scalar containing the constant parameter
estimatepublic double[] getDeviations()
confidence percent probability limits.
double array of length nPredict
containing the deviations from each forecast that give the
confidence percent probability limitspublic double[] getMA()
double array of length q containing
the final moving average parameter estimatespublic double getMeanEstimate()
z.
double scalar containing an update of the mean of
the time series z. If the time series is not
centered about its mean, and least-squares algorithm is used,
zMean is not used in parameter estimation.public double[][] getParamEstimatesCovariance()
double matrix of dimensions of np by
np, where np = p + q + 1 if
z is centered about zMean, and
np = p + q if z is not centered,
containing the covariances of parameter estimates. The ordering
of variables is zMean, ar, and
ma.public double[] getPsiWeights()
double array of length nPredict
containing the psi weights of the infinite order moving average
form of the model.public double[] getResidual()
double array of length z.length -
Math.max(arLags[i]) + length containing the residuals
(including backcasts) at the final parameter estimate point in
the first z.length - Math.max(arLags[i]) + nb,
where nb is the number of values backcast. This
method is only applicable using least-squares algorithm.public double getSSResidual()
double scalar containing the sum of squares of
the random shock, residual is the array return from the
getResidual method and na = residual.length
. This method is only applicable using least-squares
algorithm.public double getVariance()
z.
double scalar containing the variance of the time
series zpublic void setARLags(int[] arLags)
arLags - an int array of length p
containing the order of the autoregressive parameters.
The elements of arLags must be greater than
or equal to 1. Default: arLags = [1, 2, ...,
p]
public void setBackcasting(int length,
double tolerance)
length - an int scalar containing the maximum length
of backcasting and must be greater than or equal to 0.
Default: length = 10.tolerance - a double scalar containing the
tolerance level used to determine convergence of the
backcast algorithm. Typically, tolerance
is set to a fraction of an estimate of the
standard deviation of the time series. Default:
tolerance = 0.01 * standard deviation
of z.public void setBackwardOrigin(int backwardOrigin)
backwardOrigin - an int scalar specifying the
maximum backward origin. backwardOrigin
must be greater than or equal to 0 and
less than or equal to z.length -
Math.max(maxar, maxma), where maxar = Math.max(arLags[i]), maxma =
Math.max(maLags[j]), and forecasts at
origins z.length - backwardOrigin
through z.length are generated.
Default: backwardOrigin = 0.public void setCenter(boolean center)
center - a boolean scalar. If false is
specified, the time series is not centered about its
mean, zMean. If true is
specified, the time series is centered about its mean.
Default: center = true.public void setConfidence(double confidence)
confidence - a double scalar specifying the
confidence percent probability limits of the
forecasts. Typical choices for confidence are 0.90,
0.95, and 0.99. confidence must be
greater than 0.0 and less than 1.0. Default:
confidence = 0.95.public void setConvergenceTolerance(double convergenceTolerance)
convergenceTolerance - a double scalar containing
the tolerance level used to determine convergence of the
nonlinear least-squares algorithm.
convergenceTolerance represents the minimum
relative decrease in sum of squares between two iterations
required to determine convergence. Hence,
convergenceTolerance must be greater than or
equal to 0. The default value is eps = 2.2204460492503131e-16.
public void setInitialEstimates(double[] ar,
double[] ma)
ar - a double array of length p
containing preliminary estimates of the autoregressive
parameters. ar is computed internally if this
method is not used. This method is only applicable using
least-squares algorithm.ma - a double array of length q
containing preliminary estimates of the moving average
parameters. ma is computed internally if this
method is not used. This method is only applicable using
least-squares algorithm.public void setMALags(int[] maLags)
maLags - an int array of length q
containing the order of the moving average parameters.
The maLags elements must be greater than or
equal to 1. Default: maLags = [1, 2, ...,
q]public void setMaxIterations(int iterations)
iterations - an int scalar specifying the maximum
number of iterations allowed in the nonlinear
equation solver used in both the method of moments
and least-squares algorithms. Default:
interations = 200.public void setMeanEstimate(double zMean)
z.
zMean - a double scalar containing an initial
estimate of the mean of the time series z.
If the time series is not centered about its mean, and
least-squares algorithm is used, zMean is
not used in parameter estimation.public void setMethod(int method)
method - an int scalar specifying the method to be
use. If ARMA.METHOD_OF_MOMENTS is
specified, the autoregressive and moving average
parameters are estimated by a method of moments
procedure. If ARMA.LEAST_SQUARES is
specified, the autoregressive and moving average
parameters are estimated by a least-squares procedure.
Default method = ARMA.METHOD_OF_MOMENTS.public void setRelativeError(double relativeError)
relativeError - a double scalar containing the
stopping criterion for use in the nonlinear
equation solver used in both the method of
moments and least-squares algorithms. Default:
relativeError = 2.2204460492503131e-14.
|
JMSLTM Numerical Library 4.0 | ||||||||
| PREV CLASS NEXT CLASS | FRAMES NO FRAMES | ||||||||
| SUMMARY: NESTED | FIELD | CONSTR | METHOD | DETAIL: FIELD | CONSTR | METHOD | ||||||||