14.7 Polygone und Polylines

Eine Polyline besteht aus einer Menge von Linien, die einen Linienzug beschreiben. Dieser Linienzug muss nicht geschlossen sein. Ist er es allerdings, so sprechen wir von einem Polygon. In Java gibt es verschiedene Möglichkeiten, Polygone und Polylines zu zeichnen. Zunächst zum Beispiel über ein Koordinatenfeld.

abstract class java.awt.Graphics

abstract void drawPolyline( int xPoints[], int yPoints[], int nPoints ) Zeichnet einen Linienzug durch die gegebenen Koordinaten in der Vordergrundfarbe. Die Figur ist nicht automatisch geschlossen, wenn nicht die Start- und Endkoordinaten gleich sind. Mit nPoint kontrollieren wir die Anzahl der gezeichneten Linien.

abstract void drawPolygon( int xPoints[], int yPoints[], int nPoints ) Zeichnet wie drawPolyline() einen Linienzug, schließt diesen aber immer gleich, indem die erste Koordinate mit der Koordinate nPoints verbunden wird.

abstract void fillPolygon( int xPoints[], int yPoints[], int nPoints ) Füllt das Polygon aus. Da eine Polyline offen ist, kann sie nicht gefüllt werden. Somit gibt es die Funktion fillPolyline() nicht.

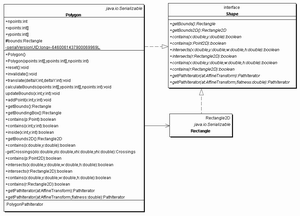
14.7.1 Die Polygon-Klasse

Neben der Möglichkeit, die Linienzüge durch Koordinatenfelder zu beschreiben, gibt es in Java die Polygon-Klasse Polygon. Sie ist eine Erweiterung des Interfaces Shape. Sie ist aber minimal, lediglich die Methode getBounds() wird implementiert. Ein Polygon-Objekt verwaltet seine Koordinaten eigenständig, und von außen können wir Elemente hinzunehmen. Mit der mächtigen Methode contains() können wir herausfinden, ob ein Punkt in der von dem Polygon ausgezeichneten Fläche liegt. Doch zunächst müssen wir ein Polygon-Objekt erzeugen. Dazu dienen zwei Konstruktoren:

class java.awt.Polygon
implements Shape, Serializable

Polygon() Erzeugt ein Polygon-Objekt ohne Koordinaten.

Polygon( int xpoints[], int ypoints[], int npoints ) Erzeugt ein Polygon mit den angegebenen Koordinaten.

Nun können wir Punkte hinzufügen und Anfragen an das Polygon-Objekt stellen:

Rectangle getBounds() Gibt die Bounding-Box der Figur zurück. Diese beschreibt ein Rechteck, das das Objekt gerade umschließt. Ein Rectangle-Objekt besitzt die Variablen height (Höhe des Rechtecks), width (Breite des Rechtecks), x (x-Koordinate) und y (y-Koordinate des Rechtecks). Mit verschiedenen Funktionen lassen sich Rechtecke zusammenfassen und schneiden.

void addPoint( int x, int y ) Die Koordinate (x,y) wird hinzugefügt. Die Grenzen (engl. boundings) werden automatisch aktualisiert.

boolean contains( int x, int y ) Liefert true, wenn der Punkt (x,y) im Polygon liegt. Es wird ein Gerade-/Ungerade-Algorithmus verwendet, um dies herauszufinden.

boolean contains( Point p ) Liefert true, wenn der Punkt p im Polygon liegt. Ein Point-Objekt besitzt die Attribute x und y für die Koordinaten.

Hier klicken, um das Bild zu Vergrößern

Das erzeugte Polygon können wir mit speziellen Methoden, natürlich aus Graphics, zeichnen.

abstract class java.awt.Graphics

void drawPolygon( Polygon p ) Zeichnet das Polygon in der Vordergrundfarbe.

void fillPolygon( Polygon p ) Zeichnet ein gefülltes Polygon.

14.7.2 N-Ecke zeichnen

Bisher gibt es im Graphics-Paket keine Funktion, um regelmäßige n-Ecke zu zeichnen. So eine Funktion ist aber leicht und schnell programmiert. Wir teilen dazu einfach einen Kreis in n Teile auf und berechnen die x- und y-Koordinate der Punkte auf dem Kreis. Diese Punkte fügen wir einem Polygon-Objekt mittels der addPoint()-Methode hinzu. Eine private Funktion drawNeck() übernimmt diese Polygon-Erstellung. Der letzte Parameter der Funktion ist ein Wahrheitswert, der bestimmt, ob das n-Eck gefüllt werden soll oder nicht. Nun kann mit zwei öffentlichen Funktionen ein nicht gefülltes beziehungsweise gefülltes n-Eck gezeichnet werden.

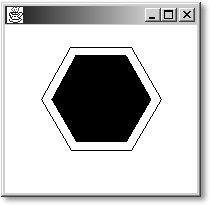
Hier klicken, um das Bild zu Vergrößern

Listing 14.8 nEck.java

import java.awt.*;
import java.awt.event.*;
public class nEck extends Frame
{
  public nEck() {
    setSize( 200, 200 );
    addWindowListener( new WindowAdapter() {
      public void windowClosing ( WindowEvent e ) {
         System.exit(0); }
      });
  }
  private void drawNeck( Graphics g, int x, int y, int r,
                         int n, boolean filled )
  {
    Polygon p = new Polygon();
    for ( int i = 0; i < n; i++ )
      p.addPoint( (int) ( x + r*Math.cos( i*2*Math.PI/n ) ),
                  (int) ( y + r*Math.sin( i*2*Math.PI/n ) ) );
    if ( filled == true )
      g.fillPolygon( p );
    else
      g.drawPolygon( p );
  }
  /**
   * Draws a n-Eck polygon with the given parameter
   */
  public void drawNeck( Graphics g, int x, int y, int r, int n )
  {
     drawNeck( g, x, y, r, n, false );
  }
  /**
   * Draws a filled n-Eck polygon with the given parameter
   */
  public void fillNeck( Graphics g, int x, int y, int r, int n )
  {
     drawNeck( g, x, y, r, n, true );
  }
  public void paint( Graphics g )
  {
    fillNeck( g, 100, 100, 50, 6 );
    drawNeck( g, 100, 100, 60, 6 );
  }
  public static void main( String args[] )
  {
    nEck poly = new nEck();
    poly.show();
  }
}

14.7.3 Vollschlanke Linien zeichnen

In Zeichenprogrammen und grafischen Präsentationen besteht häufig die Notwendigkeit, die sonst nur dünnen Standardlinien etwas aufzupusten. Es sind also dickere Linien erwünscht, und dies führt zu vielfältigen Problemen, die spontan nicht ersichtlich sind. Zunächst kommt die Frage nach der Zeichentechnik. Die erste Möglichkeit ist, mehrere Linien übereinander zu zeichnen. Dieser Ansatz ist auf den ersten Blick der einfachste, doch ein zweiter Blick auf die Grafik zeigt, dass einige Löcher entstehen; die Linien sind nicht genau übereinander. Dies liegt an den Rechenfehlern der Linienfunktion. Diese Lösung scheidet somit aus, und wir entscheiden uns für einen Linienzug, der gefüllt wird. Dies ist der einzige Ausweg. Nur ist diese Lösung nicht besonders schnell. Denn erst muss der Linienzug gezeichnet werden, und anschließend folgt eine kostspielige Füllfunktion. Doch Probleme mit Löchern gibt es nicht. Etwaigen Schwierigkeiten, wie etwa ein zwei Pixel hoher Polygonzug, in dem eigentlich kein Platz mehr ist, muss mit der Leistungsfähigkeit der Füllmethode begegnet werden.

Das zweite Problem betrifft das Ende der Linien. Sollen diese abgerundet, spitz wie ein Pfeil oder wie eine Rampe aussehen? Oder soll die Linie, die dann entsteht, einfach wie ein gedrehtes Rechteck aussehen? Ein Blick in die Grafikbibliotheken von Windows oder X11 zeigt, dass hier viele Arten existieren. Unsere folgende Funktion ist aber sehr einfach gebaut. Sie rundet nicht ab, sondern zeichnet das gedrehte Rechteck. Eine dritte Unsicherheit liegt in der Definition der Endpunkte. Ist eine Linie zehn Pixel breit, so muss sichergestellt werden, wo denn der Startpunkt liegt. Liegt er in der Mitte oder, wenn etwa die Ränder mit einer Spitze gezeichnet sind, an diesen Punkten? Da unsere Methode sehr einfach ist, kümmern wir uns nicht darum und lassen die Endpunkte mittig liegen.

public static void
drawThickLine( int x, int y, int x2, int y2, int thickness, Graphics g )
{
  int b = Math.round( thickness /2), deltax, deltay;
  double angle;
  //if (y2==y) alpha = 0; else
  angle = Math.atan( (double)((y2-y)/(x2-x)) );
  deltay = (int)Math.round( (Math.cos(angle)*b) );
  deltax = (int)Math.round( (Math.sin(angle)*b) );
  Polygon p = new Polygon();
  p.addPoint( x-deltax, y+deltay );
  p.addPoint( x+deltax, y-deltay );
  p.addPoint( x2+deltax, y2-deltay );
  p.addPoint( x2-deltax, y2+deltay );
  g.fillPolygon( p );
}

Aus der Beschreibung am Anfang geht hervor, dass das Zeichnen von dicken Linien mit den gewünschten Zusätzen wie Rändern keine triviale Aufgabe ist. Schön ist, dass sich unter der Java-2-Plattform die Java-2D-API um diese Aufgabe kümmert.