14.18 Java 2D-API

Seit dem JDK 1.2 existiert in den Java Foundation Classes (JFC) die 2D-API, mit der sich zweidimensionale Grafiken zeichnen lassen. Damit erreichen wir eine ähnliche Funktionalität wie etwa mittels der Sprache Postscript. Als wichtige Erweiterungen gegenüber den alten Zeichenfunktionen sind Transformationen auf beliebig geformten Objekten, Füllmustern und Kompositionen definiert. Die Zeichenoperationen sind optional weichgezeichnet.

Viele der 2D-Klassen sind im java.awt.geom-Paket untergebracht. Daher steht in den Programmen ganz zu Beginn:

import java.awt.geom.*;

Wenn nun die grafische Oberfläche Objekte zeichnet, wird für alle Komponenten die paint()-Methode mit dem passenden Grafikkontext aufgerufen. Unter Java 2D wurde dies um einen neuen Grafikkontext mit der Klasse Graphics2D erweitert. Um die erweiterte Funktionalität zu nutzen, muss das bekannte Graphics-Objekt in ein Graphics2D-Objekt gecastet werden.

public void paint( Graphics g )
{
  Graphics2D g2 = (Graphics2D) g;
  ...
}

Da Graphics2D eine Unterklasse von Graphics ist, lassen sich natürlich noch alle AWT-Operationen weiterverwenden.

14.18.1 Grafische Objekte zeichnen

Um in den herkömmlichen Java-Versionen grafische Primitive auf dem Schirm zu zeichnen, standen uns diverse drawXXX()- und fillXXX()-Methoden aus der Graphics-Klasse zur Verfügung. Eine blaue Linie entstand daher etwa so:

public void paint( Graphics g )
{
  g.setColor( Color.blue );
  g.drawLine( 20, 45, 324, 96 );
}

Die Methode setColor() setzt eine interne Variable im Graphics-Objekt und ändert so den Zustand. Anschließend zeichnet drawLine() mit dieser Farbe in den Speicher. Die Koordinaten sind in Pixel angegeben. Bei der 2D-API ist dies nun anders. Hier werden die Objekte in einem Kontext gesammelt und nach Bedarf gezeichnet. Der Kontext bestimmt anschließend für diese Form noch den Zeichenbereich (clipping), die Transformationen, die Komposition von Objekten und die Farben und Muster.

Das erste 2D-Programm

Beginnen wir mit einem Programm, welches eine Linie zeichnet.

Listing 14.24 First2Ddemo.java

import java.awt.*;
import java.awt.geom.*;
import javax.swing.*;
class First2DDemo extends JFrame
{
  public void paint( Graphics g )
  {
    super.paint( g );
    Graphics2D g2 = (Graphics2D) g;
    g2.setRenderingHint( RenderingHints.KEY_ANTIALIASING,
                         RenderingHints.VALUE_ANTIALIAS_ON);
    g2.draw( new Line2D.Double( 10, 40, getWidth()-10, 70 ) );
  }
  public static void main( String args[] )
  {
    JFrame f = new First2DDemo();
    f.setSize( 200, 100 );
    f.show();
  }
}

Das Programm ist wie andere AWT-Programme aufgebaut. Prinzipiell hätten wir auch Frame anstatt JFrame erweitern können. Wir erkennen auch die Umwandlung von Graphics in Graphics2D. Da normalerweise die Ausgabe nicht weichgezeichnet ist, setzen wir dies durch setRenderingHint(). Die Parameter und die Funktionen werden später näher beschrieben.

Hier klicken, um das Bild zu Vergrößern

Abbildung 14.7 Eine weiche Linie

Wirklich wichtig ist die draw()-Methode. draw() aus der Klasse Graphics2D nimmt ein Shape-Objekt und zeichnet es. Shape-Objekte sind etwa Linien, Polygone oder Kurven.

abstract class java.awt.Graphics2D
extends Graphics

abstract void draw( Shape s ) Zeichnet die Form im aktuellen Graphics2D-Kontext. Die Attribute umfassen Clipping, Transformation, Zeichen, Zusammensetzung und Stift(Stroke)-Attribute.

14.18.2 Geometrische Objekte durch Shape gekennzeichnet

Die geometrischen Objekte, die sich alle von der Klasse Shape ableiten, sind Polygon, RectangularShape, Rectangle, Area, Line2D, QuadCurve2D und CubicCurve2D. Ein Beispiel für Line2D haben wir im oberen Programm schon aufgeführt. Eine besondere Klasse, die auch von Shape abgeleitet ist, heißt GeneralPath. Damit lassen sich mehrere Objekte zu einer Figur zusammensetzen. Die Klassen sind im Paket java.awt.geom definiert.

Die Klassen Rectangle2D, RoundRectangle2D, Arc2D und Ellipse2D erben alle von der Klasse RectangularShape und sind dadurch Objekte, die von einer (mitunter virtuellen) rechteckigen Box umgeben sind. RectangularShape selbst ist abstrakt, gibt aber Methoden vor, die das Rechteck verändern und abfragen. Unter anderem gibt es Methoden, die abfragen, ob sich ein Punkt im Rechteck befindet (contains()), wie die Ausmaße sind oder wo das Rechteck seine Mitte besitzt.

Kreisiges

Die Klasse java.awt.geom.Arc2D kümmert sich um Kreisbögen. Diese Bögen werden wie bei drawArc() in einem Rechteck eingepasst und haben einen Start- und Endwert. Zusätzlich kommt ein Parameter für den Typ des Bogens hinzu. Drei Typen gibt es:

Arc2D.OPEN. Eine einfache Kreislinie

Arc2D.CHORD. Start- und Endpunkt des Bogens werden durch eine Linie verbunden.

Arc2D.PIE. Start- und Endpunkt des Bogens werden mit dem Mittepunkt des Kreises gezogen.

Listing 14.25 ArcDemo.java

import java.awt.*;
import java.awt.geom.Arc2D;
import javax.swing.JFrame;
public class ArcDemo extends JFrame
{
  public void paint( Graphics g )
  {
    Shape arc = / /       x,   y,  w,  h, start, extend, type
      new Arc2D.Double( 100, 100, 60, 60,    30,    120, Arc2D.PIE ); 
    
    ((Graphics2D)g).draw( arc );
  }
  
  public static void main(String[] args)
  {
    JFrame f = new ArcDemo();
    f.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
    f.setSize( 300, 300 );
    f.show();
  }
}

Kurven

Mit der Klasse QuadCurve2D können wir quadratische und kubische Kurvensegmente beschreiben. Dies sind Kurven, die durch zwei Endpunkte und durch dazwischen liegende Kontrollpunkte gegeben sind. Kubische Kurvensegmente werden auch Bézier-Kurven genannt.

Pfade

Eine Polygon-Klasse wie unter AWT gibt es unter der 2D-API nicht. Hier wird ein neuer Weg eingeschlagen, der über die Klasse GeneralPath führt. Damit lassen sich beliebige Formen bilden. Dem Pfad werden verschiedene Punkte zugefügt, die dann verbunden werden. Die Punkte müssen nicht zwingend wie bei Polygonen mit Linien verbunden werden, sondern lassen sich auch durch quadratische oder kubische Kurven verbinden.

Hier klicken, um das Bild zu Vergrößern

public void paint( Graphics g )
{
  Graphics2D g2 = (Graphics2D) g;
  GeneralPath p = new GeneralPath();
  p.moveTo( 10, 10 );
  p.lineTo( 100, 20 );
  g2.setColor( Color.black );
  g2.draw( p );
}

Natürlich hätten wir in diesem Fall auch ein Line2D-Objekt nehmen können. Doch dieses Beispiel zeigt einfach, wie ein Pfad aufgebaut ist. Zunächst bewegen wir den Zeichenstift mit moveTo() auf eine Position, und anschließend zeichnen wir eine Linie mit lineTo(). Um eine Kurve zu einem Punkt zu ziehen, nehmen wir quadTo() oder für Bézier-Kurven curveTo(). Die Methoden erwarten Parameter vom Typ float. Ist der Pfad einmal gezogen, zeichnet draw() die Form, und fill() füllt das Objekt aus.

14.18.3 Eigenschaften geometrischer Objekte

Windungs-Regel

Eine wichtige Eigenschaft für gefüllte Objekte ist die Windungs-Regel (engl. winding rule). Diese Regel kann entweder WIND_NON_ZERO oder WIND_EVEN_ODD sein. Konstanten aus dem GeneralPath-Objekt werden dabei einfach der Methode setWindingRule() übergeben.

p.setWindingRule( GeneralPath.WIND_NON_ZERO );

Wenn Zeichenoperationen aus einer Form herausführen und wir uns dann wieder in der Figur befinden, sagt WIND_EVEN_ODD aus, dass dann innen und außen umgedreht wird. Wenn wir also zwei Rechtecke durch einen Pfad ineinander positionieren und der Pfad gefüllt wird, bekommt die Form ein Loch in der Mitte.

Betrachten wir dazu den nachfolgenden Programmcode, der für die Mittelpunktkoordinaten x und y zwei Rechtecke zeichnet. Das erste Rechteck besitzt die Breite width sowie die Höhe height, und das innere Rechteck ist halb so groß.

GeneralPath p = new GeneralPath();
p.moveTo( x + (width/2), y - (height/2) );
p.lineTo( x + (width/2), y + (height/2) );
p.lineTo( x - (width/2), y + (height/2) );
p.lineTo( x - (width/2), y - (height/2) );
p.moveTo( x + (width/4), y - (height/4) );
p.lineTo( x + (width/4), y + (height/4) );
p.lineTo( x - (width/4), y + (height/4) );
p.lineTo( x - (width/4), y - (height/4) );

Mit moveTo() bewegen wir uns zum ersten Punkt. Die anschließenden lineTo()-Direktiven formen das Rechteck. Die Form muss nicht geschlossen werden, da dies mit fill() automatisch geschieht. Mit closePath() können wir jedoch noch zusätzlich schließen. Wenn wir das Objekt nur zeichnen, ist dies selbstverständlich notwendig. Dieses Beispiel macht durch das innere Rechteck deutlich, dass die Figuren eines GeneralPath-Objekts nicht zusammenhängend sein müssen. Das innere Rechteck wird genauso gezeichnet wie das äußere.

Mit der Konstanten WIND_NON_ZERO wird das innere Rechteck mit ausgefüllt. Ausschlaggebend dafür, ob das innere Rechteck gezeichnet wird, ist die Anzahl der Schnittpunkte nach außen - »außen« heißt in diesem Fall unendlich viele Schnittpunkte. Diese Regel wird aber nur dann wichtig, wenn wir mit nichtkonvexen Formen arbeiten. Solange sich die Linien nicht schneiden, ist dies kein Problem.

Hier klicken, um das Bild zu Vergrößern

Abbildung 14.8 Die Windungs-Regeln WIND_NO_ZERO und WIND_EVEN_ODD

Listing 14.26 WindDemo.java

import java.awt.*;
import java.awt.geom.*;
import javax.swing.*;
class WindDemo extends JFrame
{
  static GeneralPath makeRect( int x, int y, int width, int height )
  {
    GeneralPath p = new GeneralPath();
    p.moveTo( x + width/2, y - height/2 );
    p.lineTo( x + width/2, y + height/2 );
    p.lineTo( x - width/2, y + height/2 );
    p.lineTo( x - width/2, y - height/2 );
    p.closePath();
    p.moveTo( x + width/4, y - height/4 );
    p.lineTo( x + width/4, y + height/4 );
    p.lineTo( x - width/4, y + height/4 );
    p.lineTo( x - width/4, y - height/4 );
    return p;
  }
  public void paint( Graphics g )
  {
    Graphics2D g2 = (Graphics2D) g;
    g2.setRenderingHint( RenderingHints.KEY_ANTIALIASING,
                         RenderingHints.VALUE_ANTIALIAS_ON);
    g2.clearRect( 0, 0, getSize().width-1, getSize().height-1 );
    g2.setColor( Color.yellow );
    g2.fill( new Rectangle( 70, 70, 130, 50 ) );
    GeneralPath p;
    // Erstes Rechteck
    p = makeRect( 100, 80, 50, 50 );
    p.setWindingRule( GeneralPath.WIND_NON_ZERO );
    g2.setColor( Color.blue );
    g2.fill( p );
    // Zweites Rechteck
    p =  makeRect( 200, 80, 50, 50 );
    p.setWindingRule( GeneralPath.WIND_EVEN_ODD );
    g2.setColor( Color.red );
    g2.fill( p );
  }
  public static void main( String args[] )
  {
    JFrame f = new WindDemo();
    f.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
    f.setSize( 300, 150 );
    f.show();
  }
}

Das Objekt RenderingHints

Bisher haben wir stillschweigend eine Zeile eingefügt, die das Weichzeichnen (engl. antialiasing) einschaltet. Dadurch erscheinen die Bildpunkte weicher nebeneinander, sind aber etwas dicker, da in der Nachbarschaft Pixel eingefügt werden.

g2.setRenderingHint( RenderingHints.KEY_ANTIALIASING,
                     RenderingHints.VALUE_ANTIALIAS_ON );

In der Programmzeile nutzen wir die setRenderingHint()-Methode der Klasse Graphics2D. Die Methode nimmt immer einen Schlüssel (daher beginnen die Konstanten mit KEY_XXX) und einen Wert (VALUE_XXX).

abstract class java.awt.Graphics2D
extends Graphics

abstract void setRenderingHint( RenderingHints.Key hintKey, Object hintValue ) Setzt eine Eigenschaft des Rendering-Algorithmus.

Im Beispiel setzen wir den Hinweis auf das ANTIALIASING. Da durch das Weichzeichnen mehr Rechenaufwand nötig ist, empfiehlt es sich, für eine schnelle Grafikausgabe auf das Antialiasing zu verzichten. Um dies zu erreichen, würden wir den Schlüssel ANTIALIAS_OFF als zweites Argument übergeben. Weitere Hinweise sind etwa:

KEY_ALPHA_INTERPOLATION

E KEY_COLOR_RENDERING

E KEY_DITHERING

E KEY_FRACTIONALMETRICS

E KEY_INTERPOLATION

E KEY_RENDERING

E KEY_TEXT_ANTIALIASING

Mit dem RENDERING-Schlüssel können wir zum Beispiel die Geschwindigkeit bestimmen, die direkt mit der Qualität der Ausgabe korreliert. Mögliche Werte sind RENDER_SPEED, RENDER_ QUALITY oder RENDER_DEFAULT.

Dicke und Art der Linien bestimmen

Mit der 2D-API lässt sich einfach mit der Methode setStroke() die Dicke (engl. width), die Eigenschaft, wie ein Liniensegment beginnt und endet (engl. end caps), die Art, wie sich Linien verbinden (engl. line joins) und ein Linien-Pattern (engl. dash attributes) definieren.

Unterstützt wird diese Operation durch die Schnittstelle Stroke, die konkret durch BasicStroke implementiert wird. Für BasicStroke-Objekte gibt es neun Konstruktoren.

Hier klicken, um das Bild zu Vergrößern

Die folgende Anweisung zeichnet die Elemente eines Pfads mit einer Dicke von zehn Pixel:

Stroke stroke = new BasicStroke( 10 );
g2.setStroke( stroke );

Linienenden

Besonders bei breiten Linien ist es interessant, wie die Linie endet. Hier lässt sich aus CAP_BUTT, CAP_ROUND und CAP_SQUARE auswählen.

Die folgenden Zeilen aus dem Programm BasicStrokeDemo zeigen die drei Möglichkeiten auf:

g2.setStroke( new BasicStroke( 20, BasicStroke.CAP_BUTT,
                               BasicStroke.JOIN_MITER ) );
g2.drawLine( 30, 50, 200, 50 );
g2.setStroke( new BasicStroke( 20, BasicStroke.CAP_SQUARE,
                               BasicStroke.JOIN_MITER ) );
g2.drawLine( 30, 150, 200, 150 );
g2.setStroke( new BasicStroke( 20, BasicStroke.CAP_ROUND,
                               BasicStroke.JOIN_MITER ) );
g2.drawLine( 30, 100, 200, 100 );

Linien existieren aber nicht alleine, sondern sind - etwa in einem Rechteck - auch verbunden. Daher ist es wichtig, diese Eigenschaft auch bestimmen zu können. Da es keinen Konstruktor gibt, der nur den Linienende-Typ angibt, aber nicht auch gleichzeitig den Verbindungstyp, haben wir im oberen Beispiel schon eine Verbindung benutzt: JOIN_MITER. Sie ist aber nur eine von dreien. Die anderen lauten JOIN_ROUND und JOIN_BEVEL. MITER schließt die Linien so ab, dass sie senkrecht aufeinander stehen. Bei ROUND sind die Ecken abgerundet, und bei BEVEL wird eine Linie zwischen den beiden äußeren Endpunkten gezogen.

Listing 14.27 BasicStrokeDemo.java

import java.awt.*;
import javax.swing.*;
class BasicStrokeDemo extends JFrame
{
  public void paint( Graphics g )
  {
    Graphics2D g2 = (Graphics2D) g;
    g2.setRenderingHint( RenderingHints.KEY_ANTIALIASING,
                         RenderingHints.VALUE_ANTIALIAS_ON);
    g2.setStroke( new BasicStroke( 20,
                    BasicStroke.CAP_BUTT, BasicStroke.JOIN_MITER ) );
    g2.drawLine( 30, 50, 200, 50 );
    g2.setStroke( new BasicStroke( 20,
                    BasicStroke.CAP_SQUARE, BasicStroke.JOIN_MITER ) );
    g2.drawLine( 30, 150, 200, 150 );
    g2.setStroke( new BasicStroke( 20,
                    BasicStroke.CAP_ROUND, BasicStroke.JOIN_MITER ) );
    g2.drawLine( 30, 100, 200, 100 );
  }
  public static void main( String args[] )
  {
    JFrame f = new BasicStrokeDemo();
    f.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
    f.setSize( 260, 200 );
    f.show();
  }
}

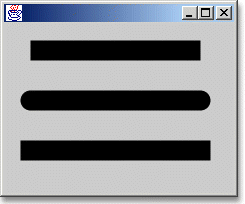
Hier klicken, um das Bild zu Vergrößern

Abbildung 14.9 Unterschiedliche Linienenden

Mit der Variablen BEVEL kann noch bestimmt werden, wie weit die Linien nach außen gezogen sind. Hier bestimmt die Variable miterlimit diese Verschiebung. Das Beispiel MiterlimitDemo.java zeigt diese Eigenschaft von miterlimit.

Listing 14.28 MiterlimitDemo.java

import java.awt.*;
import java.awt.geom.*;
import javax.swing.*;
class MiterlimitDemo extends JFrame
{
  public void paint( Graphics g )
  {
    Graphics2D g2 = (Graphics2D) g;
    g2.setRenderingHint( RenderingHints.KEY_ANTIALIASING,
                         RenderingHints.VALUE_ANTIALIAS_ON);
    BasicStroke stroke = new BasicStroke( 15,
      BasicStroke.CAP_BUTT, BasicStroke.JOIN_MITER,
      1 );  // Mitterlimit = 15
    g2.setStroke( stroke );
    g2.draw( new Rectangle2D.Float( 50, 50, 50, 50 ) );
    stroke = new BasicStroke( 15,
      BasicStroke.CAP_BUTT, BasicStroke.JOIN_MITER,
      10 );  // Mitterlimit = 15
    g2.setStroke( stroke );
    g2.draw( new Rectangle2D.Float( 150, 50, 50, 50 ) );
  }
  public static void main( String args[] )
  {
    JFrame f = new MiterlimitDemo();
    f.setSize( 250, 150 );
    f.show();
  }
}

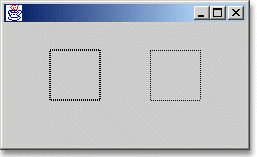
Hier klicken, um das Bild zu Vergrößern

Abbildung 14.10 Unterschiedliche Miterlimit

Füllmuster

Auch die Muster, mit denen die Linien oder Kurven gezeichnet werden, lassen sich ändern. Dazu erzeugen wir vorher ein Feld und übergeben dies einem Konstruktor. Damit auch die Muster abgerundet werden, muss CAP_ROUND gesetzt sein. Die nachfolgenden Zeilen erzeugen ein Rechteck mit einem einfachen Linienmuster. Es sollen zehn Punkte gesetzt und zwei Punkte frei sein.

float dash[] = { 10, 2 };
BasicStroke stroke = new BasicStroke( 2,
  BasicStroke.CAP_BUTT, BasicStroke.JOIN_MITER,
  1,
  dash, 0 );
g2.setStroke( stroke );
g2.draw( new Rectangle2D.Float( 50, 50, 50, 50 ) );

Als letzter Parameter hängt am Konstruktor noch eine Verschiebung. Diese bestimmt, ob im Muster Pixel übersprungen werden sollen. Geben wir dort für unser Beispiel etwa 10 an, so beginnt die Linie gleich mit zwei nicht gesetzten Pixeln. Eine 12 ergibt eine Verschiebung wieder an den Anfang. Bei nur einer Zahl im Feld ist der Abstand der Linien und die Breite einer Linie genau so lang wie diese Zahl angibt. Bei gepunkteten Linien ist das Feld also 1. Hier eignet sich ein anonymes Feld ganz gut, wie die nächsten Zeilen zeigen:

stroke = new BasicStroke( 1,
  BasicStroke.CAP_BUTT, BasicStroke.JOIN_BEVEL,
  1, new float[]{ 1 }, 0 );

Bei feinen Linien sollten wir das Weichzeichnen besser ausschalten.

Hier klicken, um das Bild zu Vergrößern

Abbildung 14.11 Zwei Linienmuster

14.18.4 Transformationen mit einem AffineTransform-Objekt

Eine affine Transformation eines Objekts ist entweder eine Translation (Verschiebung), Rotation, Skalierung oder Scherung¹. Bei diesen Transformationen bleiben parallele Linien nach der Transformation auch parallel. Um diese Operationen durchzuführen, existiert eine Klasse AffineTransform. Dem Graphics2D-Kontext können diese Transformationen vor dem Zeichnen zugewiesen werden, etwa über die Methode setTransform(). Aber auch Grafiken kann mit drawImage() vor dem Zeichnen ein AffineTransform-Objekt übergeben werden. Auf diese Art können sie auch einfach bearbeitet werden. Mit wenigen Zeilen Programmcode lassen sich dann beliebige Formen, Texte und Grafiken verändern.

Die zweidimensionalen Objekte können durch die Operationen Translation, Rotation, Skalierung oder Scherung verändert werden. Diese Operationen sind durch eine 3x3-Matrix gekennzeichnet. Die Klasse AffineTransform bietet nun Methoden an, damit wir diese Matrix selbst erzeugen können, sowie Hilfsmethoden, die uns die Arbeit abnehmen.

AffineTransform trans = new AffineTransform();
trans.rotate( 0.1 );
g2.setTransform( trans );
g2.fill( new Rectangle2D.Float( 150, 100, 60, 60 ) );

Hier klicken, um das Bild zu Vergrößern

Konstruktoren

Die Klasse AffineTransform besitzt sechs Konstruktoren: zunächst einen Standard-Konstruktor und einen Konstruktor mit einem schon vorhandenen AffineTransform-Objekt, dann jeweils einen Konstruktor für eine Matrix mit dem Datentyp float und mit dem Datentyp double sowie zwei Konstruktoren mit allen sechs Werten der Matrix für float und double. Eine eigene Matrix macht nur dann Sinn, wenn wir mehrere Operationen hintereinander ausführen lassen wollen. So nutzen wir in der Regel den Standard-Konstruktor wie oben und ändern die Form durch die Methoden rotate(), scale(), shear() oder translate(). Wird nach dem Erzeugen des AffineTransform-Objekts direkt eine der Methoden aufgerufen, geht dies auch einfacher über die statischen Erzeugungsmethoden getRotateInstance(), getScaleInstance(), getShearInstance() und getTranslateInstance(). Sie füllen dann die Matrix mit den passenden Einträgen. Ein Transformationsobjekt kann mit setToIdentity() wieder initialisiert werden, so dass AffineTransform wiederverwendbar ist.

¹ Ein Objekt wird geschert, wenn es entlang einer Koordinatenachse verzogen wird. Im Zweidimensionalen gibt es zwei Scherungsarten: entlang der x-Achse und entlang der y-Achse.